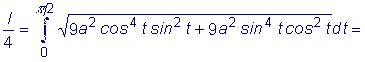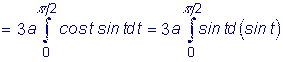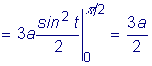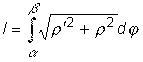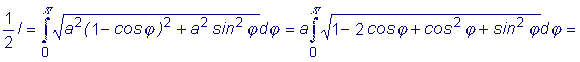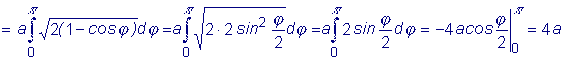Темы | Предыдущий пункт | Следующий пункт | Литература
Лекция 5.2.

Приложения определенного интеграла.

5.2.4. Длина дуги кривой.

 

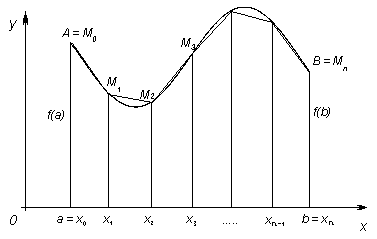
Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной возрастает неограниченно, а длина наибольшего звена стремится к нулю.

Кривая называется гладкой, если она непрерывна и в каждой точке имеет касательную, непрерывно меняющую свое положение от точки к точке. Рассмотрим вопрос о длине дуги l кривой, заданной функцией y = f(x),.

A = M0 ; M1 ; M2 ; ... ; Mn-1 ; Mn = B 

Проектируя точки Mi ось Ox получим разбиение отрезка [a, b] на n частей .

Рассмотрим i -тое звено ломаной , где - приращение функции f(x) на .
:



Согласно теореме Лагранжа:

, .

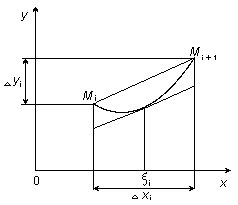
Тогда:

,

а длину всей ломаной можно получить суммируя все её звенья.

.

Перейдем к пределу, считая, что длина наибольшего звена стремится к нулю.

(1)

Пример:

Найти длину дуги кривой между точками с абсциссами x1 = 3 и x2 = 8.
Согласно формуле (1) имеем:
.

Длина дуги кривой, заданной в параметрическом виде.

Пусть линия задана в параметрическом виде, то есть

, 

где и непрерывно дифференцируемые на отрезке [t1, t2] функции.

При стремлении отрезка ломаной к нулю можно считать, что , то есть является дифференциалом дуги. Аналогично , соответствующие дифференциалы.

Тогда можно записать:
(2)

Эта формула для вычисления дифференциала дуги.
Так как и , то
, 
(3)

Пример:

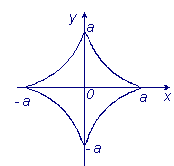
Найти длину дуги астроиды .     

,




Длина дуги в полярных координатах.

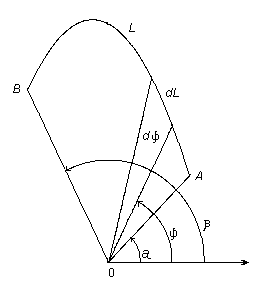
Выведем сначала дифференциал дуги dl в полярных координатах. Из предыдущего раздела известно, что , где x и y прямоугольные декартовы координаты точки дуги.
Как известно, формулы перехода от полярных координат и к прямоугольным x и y следующие:

и . 

Тогда:


.
Возводя в квадрат и складывая получим:
Cледовательно:

(*)
Для того чтобы найти длину дуги непрерывно дифференцируемой кривой между точками А и В  необходимо проинтегрировать равенство (*) в пределах от до .
(4)

Пример:

Вычислить полную длину дуги кардиоиды (см. 5.2.2, пример 1) .
 

В силу симметрии запишем:


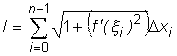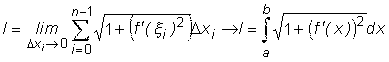
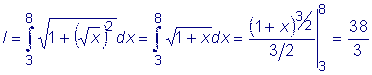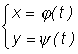
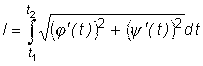
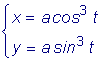Задачи для самостоятельного решения.