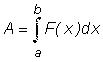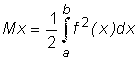Темы | Предыдущий пункт | Следующая лекция | Литература
Лекция 5.2.

Приложения определенного интеграла.

5.2.5. Физические и механические приложения определенного интеграла.

Одно из основных применений определенного интеграла - вычисление работы переменной силы.
Задача.
Вычислить работу А непрерывной переменной силы F(x), приложенной к материальной точке М, при перемещении последней вдоль оси Ox из положения x = a в положение x = b, предполагая, что направление силы совпадает с направлением перемещения.

Рис. 1


Пусть точка М переместилась из положения x в положение x + dx (Рис. 1) На бесконечно малом промежутке [x, x + dx] длины dx cилу F(x) приближенно можно считать постоянной. Поэтому элементарная работа силы равна:
dA = F(x)dx
Интегрируя данное выражение в пределах от x = a до x = b, получим всю работу:

(1)

Кроме того, определенный интеграл применяется для вычисления некоторых механических величин, например: статических моментов, координат центра масс криволинейной трапеции:
Статический момент относительно оси ОХ: 

(2)

Статический момент относительно оси OY:

(3)

Координаты центра масс:

(4)

где S - площадь криволинейной трапеции.

Задачи для самостоятельного решения.