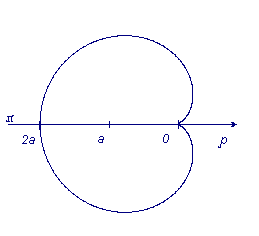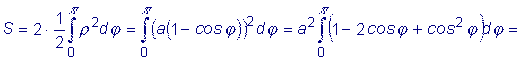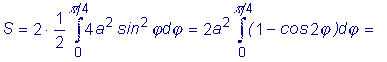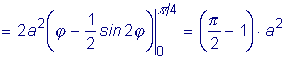Темы | Предыдущий пункт | Следующий пункт | Литература
Лекция 5.2.

Приложения определённого интеграла

5.2.2. Площадь в полярных координатах.

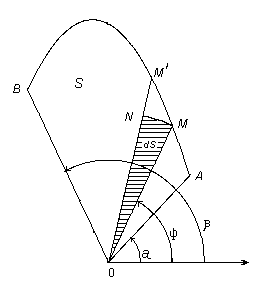
Задача 1. Найти площадь S сектора OAB, ограниченной данной линией и двумя лучами , , где и - полярные координаты.


Для решения задачи разобьем сектор AOB на секторы лучами

.
Элемент n-ого сектора можно приближенно считать круговым сектором, ограниченным окружностью радиуса . Площадь такого сектора:

. 

Чтобы получить общую площадь суммируем площади всех полученных секторов.
.

Таким образом, получаем формулу для вычисления площади в полярных координатах:

 

 

Пример 1:

Вычислить площадь фигуры, ограниченной координатой


Учитывая симметрию фигуры можно записать:

Пример 2:

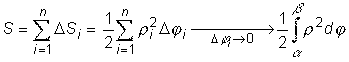Вычислить площадь фигуры, ограниченной дугами окружностей и  


Окружности пересекаются при ; рассматриваемая фигура симметрична относительно , следовательно её площадь можно вычислить так: