| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Приложения определённого интеграла. |
|
|
|
||||
|
5.2.3. Вычисление объемов тел вращения |
||||
|
Пусть L есть кривая y = f(x),
Аналогично можно получить формулу объема тела вращения вокруг оси OY.
Пример: Вычислить объем тела, полученного вращением вокруг оси Oy фигуры Ф, лежащей в плоскости Oxy и ограниченной линиями y2 = 4 - x, x = 0
|
||||
|
|
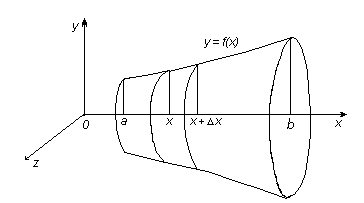
 приближенно выражает V. При
переходе к пределу получим формулу объема тела вращения:
приближенно выражает V. При
переходе к пределу получим формулу объема тела вращения:
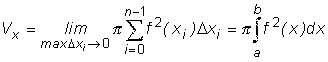

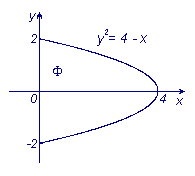
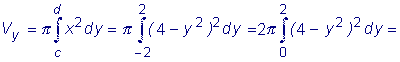
 .
.