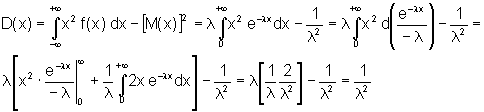В этих задачах важной характеристикой является интенсивность отказа (коэффициент смертности)  исследуемых элементов.  Введем его следующим образом. Пусть А - событие, обозначающее безотказную работу объекта на промежутке времени (0, t); В - событие, обозначающее безотказную работу на промежутке (t, t₁). Тогда вероятность того, что объект не откажет на промежутке времени (t,t₁), если он безотказно проработал до момента времени t, есть условная вероятность

Так как событие АВ обозначает безотказную работу элемента на (0,>t₁), вероятность отказа на    (t, t₁) выразится следующим образом

.

Положим теперь  и устремим  к нулю. Тогда

,

где  при . 

Введем обозначение

.                                                                                                                              (1)

Эта величина  является локальной характеристикой надежности и называется интенсивностью отказов. Физический смысл  заключается в том, что она есть вероятность того, что объект, проработавший безотказно до момента t, откажет в последующую единицу времени (если эта единица мала). В терминах теории вероятностей  есть плотность условной вероятности отказа в момент t, при условии, что до этого времени объект работал безотказно. Этот показатель широко используют при обработке результатов ресурсных испытаний или наблюдений над объектом в процессе эксплуатации.

Рис.1.

Типичная кривая изменения интенсивности отказов во времени приведена на рис. 1. на ней четко выражены три характерных периода работы объекта. Период приработки (обкатки) (0, t₁) связан с наличием явных и скрытых дефектов, которые приводят к относительно быстрому выходу из строя этих элементов. Период нормальной эксплуатации (t₁,t₂), во время которого происходят главным образом случайные отказы (аварии, несчастные случаи и т. п.) Последний период эксплуатации (жизни) объекта - период старения и износа, когда необратимые явления приводят к ухудшению качества объекта, к его <старению>. Каждому периоду соответствует свой вид функции . На участке нормальной эксплуатации во многих случаях интенсивность отказов постоянна.

Если интенсивность отказов  задана, то соотношение (1) можно рассматривать как дифференциальное уравнение относительно функции P(t). Решая его, получим

.

Если Р(0) = 1, то

.

Рассмотрим частный случай, когда интенсивность отказов . Тогда

.

Получаем так называемый экспоненциальный закон надежности. Для него вероятность отказа за время t равна

.

Функция плотности вероятности отказов

.

Экспоненциальный закон надежности широко применяется в прикладных расчетах благодаря его физической простоте и удобству использования. Для этого закона справедливо следующее важное свойство: если вероятность безотказной работы на данном интервале не зависит от времени предшествующей работы, а только от длины интервала, то этот закон обязательно будет экспоненциальным. Это свойство является необходимым и достаточным. Необходимость следует из того, что вероятность безотказной работы на промежутке  по формуле (19.15) равна

.

Таким образом экспоненциальный закон описывает надежность нестареющих объектов, отказ которых носит случайный характер, обусловленный сочетанием внешних и внутренних факторов. Например, прокол шины при случайном наезде на гвоздь при условии , что износ мало влияет на ее сопротивление проколу. Если данные эксплуатации хорошо согласуются с экспоненциальным законом, то можно утверждать, что характеристики (механические и т. п.) на участке, где , почти не изменяются. Это имеет большое значение для анализа состояния объекта исследования.

В общем случае показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

где  - постоянная положительная величина.

Это распределение определяется одним параметром . Функция распределения имеет вид

Графики функций f(x) и F(x) приведены на рисунках 2 и 3.

Рис. 2.		Рис.3.

Найдем числовые характеристики показательного распределения