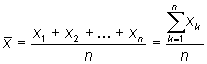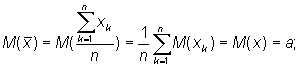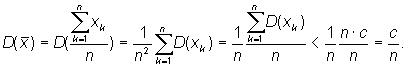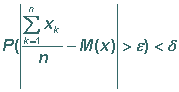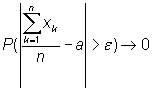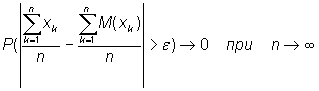| Темы | Следующий пункт | Литература |
|
|
 Предельные
теоремы теории вероятностей
Предельные
теоремы теории вероятностей
|
|
13.6.1 Закон больших чисел Предельные теоремы устанавливают зависимость между случайностью и необходимостью, что позволяет научно предсказывать результаты будущих испытаний, связанных с изучением закономерностей массовых случайных явлений. Они делятся на две группы, одна из которых получила название закона больших чисел, а другая – центральной предельной теоремы. Закон больших чисел состоит из нескольких теорем, в которых доказывается приближение средних характеристик при соблюдении определенных условий к некоторым постоянным значениям. Содержательные результаты в теории вероятностей могут быть получены, если рассматривать не одно событие или случайную величину, а много. О большом числе случайных событий можно сделать некоторые практически достоверные выводы. Аппарат, позволяющий получать выводы о вероятностях разных событий, связанных с большим числом случайных величин включает в себя теорему о том, что дисперсия суммы независимых случайных величин равна сумме их дисперсий, и неравенство Чебышева. Неравенство ЧебышеваПусть случайная величина Х имеет конечные математическое ожидание М(х) и дисперсию D(x). Если дисперсия мала, то большие отклонения Х от М(х) маловероятны (дисперсия есть мера отклонения случайной величины от математического ожидания). Этот факт выражается теоремой.
Теорема. Вероятность
того, что отклонение случайной
величины Х, имеющей конечные М(х)
и D(x), от ее
математического ожидания М(х) по
абсолютной величине превзойдет любое
наперед заданное положительное число
Это неравенство называется неравенством Чебышева. Утверждение, содержащееся в неравенстве Чебышева, опирается только на значение дисперсии, не используя сведения о конкретном виде закона распределения, поэтому дает лишь грубые оценки сверху для вероятностей событий вида
Например, если положить
Если полагать, что Х подчиняется нормальному закону распределения, то значение этой же вероятности, вычисленное с помощью таблиц равно 0,0027, что в 40 раз меньше ее оценки, полученной на основании неравенства Чебышева. В то же время следует иметь в виду, что вероятности рассматриваемых событий не могут превышать значений, вычисленных по неравенству Чебышева ни при каком законе распределения. Замечание.
Если в неравенстве Чебышева положить
У
= Х – М(Х), то
D(X) = MY2
и это неравенство примет вид
Для правильной организации сборки узла
необходимо оценить вероятность, с
которой размеры деталей отклоняются от
середины поля допуска не более чем на 2
мм. Известно, что середина поля допуска
совпадает с математическим ожиданием
размеров обрабатываемых деталей, а
среднее квадратическое отклонение
равно 0,25 мм.
Решение
По
условию задачи имеем Давно
замечено, что хотя результаты
отдельных измерений В условии теоремы
вводятся некоторые
ограничения на случайные величины Вторая группа – предположения о независимости
величин С учетом этих
предположений образуем новую
случайную величину
как среднюю арифметическую
этих случайных величин. Используя
свойства математического ожидания и
дисперсии случайных величин, получим
Применим к случайной
величине Выбрав число n
членов в средней арифметической,
достаточно большим, получим, что число может быть
сделано сколь угодно малым.
Таким
образом доказана следующая теорема
Теорема
Чебышева
При
достаточно большом числе независимых
испытаний n можно с
вероятностью, близкой к нулю,
утверждать , что абсолютная величина
разности между средним арифметическим
наблюдавшихся значений случайной
величины Х и математическим
ожидание этой величины окажется больше
заданного числа Это утверждение равносильно
тому, что
с
возрастанием n,
где а = М(х).
Теорема
Чебышева позволяет с достаточной
точностью по средней арифметической
судить о математическом ожидании и
наоборот. Так, на основании теоремы
можно утверждать, что если произведено
достаточно большое количество
измерений некоторого параметра
прибором без систематической
погрешности, то средняя арифметическая
результатов этих измерений сколь
угодно мало отличается от истинного
значения измеряемого параметра.
Теорема
Чебышева распространяется и на случай n
попарно независимых случайных величин
Пример Для определения потребности в жидком металле и сырье выборочным путем устанавливают средний вес отливки гильзы к автомобильному двигателю, так как вес отливки, рассчитанный по металлической модели отличается от фактического веса. Сколько нужно взять отливок, чтобы с вероятностью, большей 0,9 , можно было утверждать, что средний вес отобранных отливок отличается от расчетного, принятого за математическое ожидание веса, не более чем на 0,2 кг? Решение
Согласно условию задачи, имеем
где Следовательно Откуда находим n > 50. Теорема Бернулли Теорема Бернулли устанавливает связь между частотой появления события и его вероятностью, то есть объясняет эффект устойчивости относительных частот. Эта теорема может быть получена как следствие из теоремы Чебышева.
Теорема При
достаточно большом числе независимых
испытаний вероятность того, что
частота появления события А в этих
испытаниях, отличается от его
вероятности по абсолютной величине
больше, чем на любое число
При решении практических
задач иногда бывает необходимо оценить
вероятность наибольшего отклонения
частоты появления события от ее
ожидаемого значения. Случайной
величиной в этом случае является число
появления события А в n
независимых испытаниях:
Используя неравенство
Чебышева, получим
Пример
Из 1000
изделий, отправляемых в сборочный цех,
было подвергнуто обследованию 200
отобранных случайным образом изделий.
Среди них оказалось 25 бракованных.
Приняв долю бракованных изделий среди
отобранных за вероятность
изготовления бракованного изделия,
оценить вероятность того, что во всей
партии бракованных изделий окажется не
более 15 % и не менее 10%.
Решение
Находим вероятность
изготовления бракованного изделия
Наибольшее отклонение
частоты появления бракованных изделий
от вероятности р по абсолютной
величине равно
число испытаний n = 1000.
Используя формулу
|
|
|
|
|