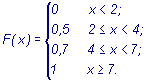Пусть Х – случайная величина, а х – ее допустимое значение. Предположим, что случайная величина может принимать любые действительные значения от до .

Это предположение не ограничивает общности, так как изменение случайной величины в ограниченном интервале значений будет означать, что вероятность попадания ее в любую область числовой оси вне указанного интервала равна нулю. В случае дискретной случайной величины, отличные от нуля вероятности соответствуют конечному или счетному множеству дискретных точек на числовой оси.

Используем следующее правило разбиения: фиксируем некоторый уровень х, и область возможных значений случайной величины делится на две части. К одной относятся значения Х не превосходящие х, а к другой – остальные. 

Функция

показывающая как зависит от величины выбранного уровня вероятность того, что значения случайной величины не превосходят этот уровень, называется функцией распределения вероятностей (иногда ее называют интегральной функцией распределения).

Требование, чтобы функция распределения вероятностей F(x) представляла собой вероятность, накладывает на ее свойства определенные ограничения. 

Свойства функции распределения 

• Функция распределения F(x) есть неотрицательная функция, заключенная между нулем и единицей:

  .

• Вероятность попадания случайной величины Х в интервал равна разности значений функции распределения на концах этого интервала   

  .

• Функция распределения случайной величины есть неубывающая функция, то есть

  при .

• Функция распределения F(x) стремится к нулю при неограниченном уменьшении Х и стремится к единице при неограниченном возрастании Х, то есть

    и 

Для дискретной случайной величины Х, которая может принимать значения , функция распределения имеет вид

где суммирование распространяется на все те значения х_i, которые по своей величине меньше х.

Справедливо обратное утверждение. Зная функцию распределения вероятностей F(x) можно определить вероятность Р(х_к) дискретной случайной величины

где

Иначе говоря, задание закона распределения вероятностей при помощи функции распределения позволяет перейти к любой другой его форме.

Пример

Дискретная случайная величина Х задана законом распределения

 

Х	2	4	7
р	0,5	0,2	0,3

Найти функцию распределения F(x) и начертить ее график.

Решение. 

Если х < 2, то величина Х значений меньше 2 не принимает и

Если , то х может принять значение 2 с вероятностью 0,5. F(x) = 0,5.

Если , то .

Если , то .

Следовательно,

График этой функции имеет вид