Лекция 13.4

Случайные величины

13.4.1  Случайные величины. Основные понятия

До сих пор мы рассматривали случайные события, которые качественно характеризуют результат эксперимента. На практике часто результат эксперимента представляют количественно в виде некоторой действительной величины, которая называется случайной величиной.

С точки зрения инженерного подхода случайная величина – это просто числовое описание исхода случайного эксперимента. Пространство событий представляет собой множество всех возможных исходов эксперимента. При исходе случайная величина Х принимает значение, которое можно обозначить Х() 

При таком подходе случайная величина – просто действительная функция, определенная на пространстве элементарных событий.

Случайные величины обозначают большими буквами латинского алфавита  X, Y, Z…, а возможные их значения – соответствующими малыми буквами x, y, z. Случайная величина, множество возможных значений которой конечно или счетно, называется дискретной случайной величиной. Например, число дефектных изделий в партии; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов устройства за определенный промежуток времени его работы и т. д.

Случайная величина, способная принимать любые значения из некоторого конечного или бесконечного интервала называется непрерывной случайной величиной. Например, время безотказной работы как отдельных элементов системы, так и всей системы в целом; размеры детали, обработанной на токарном станке, сила тока или напряжение в электрической сети, температура воздуха в различное время суток и т. д.

В простейшем случае, когда в результате эксперимента может появляться или не появляться событие А, этому случайному событию можно поставить в соответствие случайную величину, принимающую только два значения 1 или 0 в зависимости от того, произошло или не произошло событие А. Тогда вероятность того, что случайная величина примет значение, равное 1, совпадает с вероятностью появления события А. В схеме независимых испытаний Бернулли множество состоит из элементарных событий , где 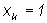если при k - ом испытании произошел успех, и в случае неуспеха. 

Случайная величина 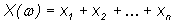равна числу успехов при n испытаниях в схеме Бернулли. Любую константу С можно рассматривать как частный случай случайной величины. Такие случайные величины называют вырожденными.

Таким образом, если в результате эксперимента может появиться событие из конечной или бесконечной (счетной) совокупности событий, то такой группе событий будет соответствовать некоторая дискретная случайная величина, возможные значения которой можно пронумеровать с помощью целых чисел. Вероятность того, что дискретная случайная величина примет одно из возможных значений, равна вероятности появления случайного события, соответствующего этому значению.

Однако понятие случайной величины является более общим, чем понятие случайного события. Так, в случае непрерывной случайной величины ее возможные значения непрерывно заполняют конечный или бесконечный интервал действительной оси. Говорить о вероятности данной величины не имеет смысла, так как эта вероятность равна нулю. Можно, однако, разбить интервал возможных значений случайной величины на конечное число непересекающихся отрезков. Тогда совокупность событий, состоящих в том, что случайная величина попадет в любой из этих отрезков, образует полную группу. При этом введение понятия вероятности того, что значения случайной величины находятся в пределах некоторого отрезка, становится совершенно аналогичным дискретному случаю.

Однако для технических приложений обычно нет необходимости рассматривать в явном виде пространство событий. Достаточно уметь приписывать вероятности различным событиям, связанным с рассматриваемыми случайными величинами.

Правило, согласно которому каждому возможному значению дискретной случайной величины или некоторой области значений непрерывной случайной величины ставится в соответствие вероятность того, что случайная величина примет определенные значения или будет находиться в некоторой области интервала возможных значений, называется законом распределения вероятностей случайной величины. Дискретную случайную величину можно задать таблицей, в одной строке которой записаны возможные значения х_к, принимаемые случайной величиной Х, а в другой – соответствующие им вероятности Р_к.

Х1	Х2	...	Хk	...	Хn
P1	P2	...	Pk	...	Pn

Так как объединение всех возможных событий 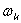, заключающихся в том. Что случайная величина Х примет значения, равные х_к (к = 1, 2, …, n), есть событие достоверное, то имеем условие

.

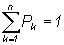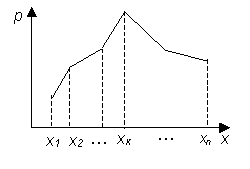
При графическом изображении закона распределения дискретной случайной величины в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат соответствующие вероятности. Затем строят точки (х_к, р_к) и соединяют их прямолинейными отрезками. Полученная фигура называется многоугольником распределения.

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины называют зависимыми.

Аналитическим выражением законов распределения являются функции распределения. Способ определения законов распределения вероятностей, указанный выше, однозначен для дискретных случайных величин и неоднозначен для непрерывных. В последнем случае остается совершенно произвольным правило разбиения интервала на конечное число непересекающихся отрезков. Рассмотрим общепринятый подход к определению закона распределения, справедливый для случайных величин дискретных и непрерывных. В основе этого подхода лежит использование так называемой функции распределения.