| Темы | Предыдущий пункт | Следующий пункт | Литература |
|
|
 Случайные
величины
Случайные
величины
|
|
13.4.3 Плотность распределения вероятностей Хотя функция распределения
и дает исчерпывающее описание
вероятностной модели одной случайной
величины, ее форма не всегда удобна для
выполнения необходимых расчетов. В
случае непрерывной и дифференцируемой
функции распределения (за исключением
может быть дискретных точек) иногда
предпочтительнее использовать не саму
функцию F(x), а ее
производную
Поскольку f(x) – плотность распределения вероятностей, а не сама вероятность, то она не должна быть обязательно меньше 1 и может принимать любые неотрицательные значения. Иногда f(x) называют дифференциальной функцией распределения. Для описания распределения вероятностей дискретной случайной величины функция плотности распределения неприменима. Свойства функции плотности распределения.
 . .
Геометрически это означает, что площадь, ограниченная кривой распределения f(x) и осью абсцисс, равна 1 Пример Случайная величина подчинена закону распределения с плотностью 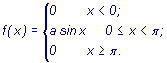 Определить коэффициент а,
построить график плотности
распределения. Найти вероятность
попадания случайной величины на
участок от 0 до
Определить коэффициент а,
построить график плотности
распределения. Найти вероятность
попадания случайной величины на
участок от 0 до
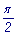 . Определить
интегральную функцию и построить ее
график. . Определить
интегральную функцию и построить ее
график.
Решение. Площадь, ограниченная кривой распределения численно равна
Следовательно, плотность распределения примет вид
График плотности распределения изображен на рисунке
Таким образом, функция распределения имеет вид
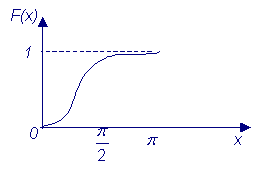
График ее изображен на рисунке
Модой М случайной величины называют такое значение х, при котором f(x) = maxМедианой Ме случайной величины называют такое х = Ме, для которого
то есть для которого левая и правая площади под кривой плотности вероятности одинаковы. Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1, то функция распределения в точке, соответствующей медиане, равна 0,5
|
|
|
|
|
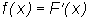 ,
называемую плотностью
распределения вероятностей. Этот
термин становится понятным, если
рассмотреть непрерывную случайную
величину Х в достаточно узких границах
от х до
,
называемую плотностью
распределения вероятностей. Этот
термин становится понятным, если
рассмотреть непрерывную случайную
величину Х в достаточно узких границах
от х до 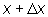 .
Тогда
.
Тогда

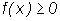 .
.
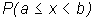 численно равна площади
криволинейной трапеции,
изображенной на рисунке
численно равна площади
криволинейной трапеции,
изображенной на рисунке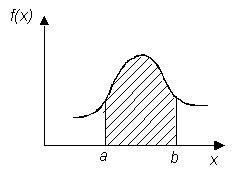
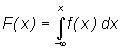
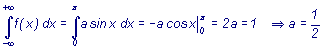
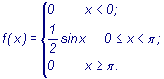
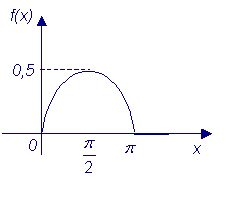
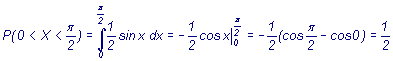

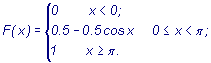
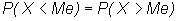 ,
,