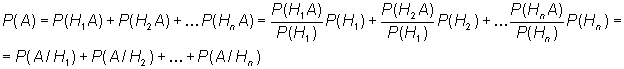ODE Lecture 6.1.

Темы | Предыдущий пункт | Следующий пункт | Литература

Лекция 13.2

Вероятность сложность событий

13.2.2 Формула полной вероятности

Предположим, что некоторое событие А может наступить только при условии появления одного из событий , образующих полную группу несовместных событий (называемых гипотезами). Это означает, что А можно представить в виде суммы несовместных событий:

где - достоверное событие. По теореме сложения вероятностей можно записать

Таким образом, получим формулу

Эта формула называется формулой полной вероятности и широко применяется в теории вероятностей и ее приложениях. Применимость этой формулы можно обосновать тем, что эксперимент со случайным исходом распадается на два этапа: в первом «разыгрываются» условия эксперимента, во втором – его результат.

Пример 1.

На сборочный конвейер поступают детали с трех станков. Производительность станков неодинакова. Первый дает 50% программы, второй – 30%, а третий – 20%. Если в сборку поступает деталь, сделанная на первом станке, то вероятность получения годного узла равна 0,98. Для продукции второго и третьего станков соответствующие вероятности равны 0,95 и 0,8. Определить вероятность того, что узел, сходящий с конвейера годный.

Решение
Введем обозначения: А – событие, означающее годность узла, - события, означающие, что детали сделаны соответственно на первом, втором и третьем станках. Тогда

Искомая вероятность по формуле полной вероятности равна

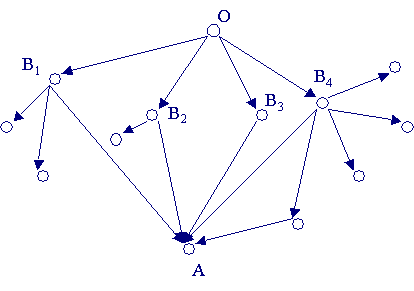
Пример 2.

Пешеход, идущий из некоторого пункта О в пункт А, стоит на разветвлении дорог и выбирает наугад один из возможных путей. Схема дорог изображена на рисунке. Какова вероятность того, что пешеход попадет в пункт А.

Решение

Из схемы видно, что путь пешехода обязательно проходит через один из промежуточных пунктов . Обозначим через событие, состоящее в том, что при своем движении пешеход попадет в пункт . События образуют полную систему и очевидно, что они равновероятны (по условию один из путей выбираются произвольно). Поэтому

.

Если пешеход попадет в пункт , то он сможет прийти в пункт А, выбрав одно из трех равновозможных направлений движения. Обозначим через А событие, состоящее в том, что пешеход приходит в пункт А. Тогда условная вероятность прийти в А из пункта равна . Аналогично

По формуле полной вероятности

.