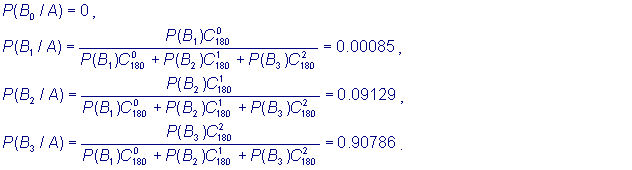Темы | Предыдущий пункт | Следующий пункт | Литература
Home page Home page Лекция 13.2

Вероятность сложность событий

13.2.3  Формула Байеса

В прикладных задачах возможны следующие ситуации. На начальной стадии изучения какого либо явления исследователь, обладающий определенной квалификацией и опытом подобных прошлых работ, имеет некоторое представление о свойствах объекта исследования. В это представление входят эмпирические данные, полученные ранее при аналогичных исследованиях. В ходе испытания объекта появляется новая информация в виде совокупности эмпирических данных, которые изменяют представление (вероятностное) о свойствах объекта. Происходит пересмотр и переоценка априорного представления.

Предположим, что до эксперимента о его условиях можно высказать ряд гипотез , несовместных и образующих полную группу .

Вероятности гипотез до эксперимента (априорные вероятности) известны .

Эти события (гипотезы) непосредственно не наблюдаемы, но можно наблюдать некоторое событие А, с ними связанное, для которого известны условные вероятности .  Вероятности гипотез кажутся недостаточно надежными, поэтому для их уточнения проводим эксперимент в результате которого появилось событие А. Требуется пересмотреть вероятности гипотез с учетом этого факта, т.е. найти «апостериорные» вероятности гипотез.

Вероятность совместного наступления событий на основании правила умножения вероятности равна:

.

Отсюда следует

.

Заменяя  по формуле полной вероятности, получим

.

Эта формула называется формулой Байеса. Она решает поставленную задачу – позволяет перейти от априорной информации, формализованной в виде априорного распределения, к апостериорной путем добавления эмпирических данных (распределением вероятностей называют соответствие между событиями и их вероятностями). Этот процесс может быть продолжен с получением нового эмпирического результата. По мере накопления выборочной информации она начинает преобладать а в апостериорном распределении. При этом если два исследователя располагали различными априорными распределениями (в силу различной первоначальной информации) их апостериорные распределения будут сближаться.

Формулы Байеса находят широкое применение при решении проблем управления, связанных с принятием административных решений, когда приходится сталкиваться с недостаточной информацией о закономерностях в экономике и промышленности. По мере накопления дополнительной информации производится корректировка решения. Одной из таких проблем является принятие окончательного решения при входном контроле партии деталей. При этом возможны следующие варианты решений:

  1. Принять всю партию, запустив ее в производство;
  2. Проконтролировать каждое изделие в партии, заменяя или исправляя при этом дефектные изделия;
  3. Забраковать всю партию.

Рассмотрим следующий пример. Пусть на завод поставляют партии изделий объемом N. Обозначим через наличие в партии i бракованных изделий (i= 0, 1, 2, …, l). При контроле из партии случайным образом отбирается n изделий. Обозначим через А событие, означающее наличие в выборке бракованных изделий. Вероятность обнаружения k бракованных изделий среди n отобранных (k = 0, 1, 2, …, m), если во всей партии содержится i бракованных изделий, определим по формуле 

.

Условную вероятность  находим по формуле Байеса

Пример 1.

Пусть по проведенным ранее выборкам известно, что в поставляемых с завода – изготовителя партиях имеется следующее распределение количества колец, не удовлетворяющих принятому уровню качества
Количество бракованных колец в партии 0 1 2 3
Вероятность наличия в партии i бракованных колец 0,5 0,3 0,18 0,02

При входном контроле партии из 200 колец в выборке объемом 20 единиц обнаружено одно поршневое кольцо ниже принятого уровня качества. Оценить вероятность наличия дефектных изделий в партии после входного контроля. 

Решение.

По условию задачи имеем: N = 200, n = 20, k = 1,

Вероятности наличия дефектных изделий в партии будут:

Переоценка вероятностей позволяет администрации, исходя из экономических затрат, либо забраковать партию колец, отправив ее на завод – изготовитель, либо произвести разбраковку партии, либо принять ее в производство.

Пример 2.

Объект, за которым ведется наблюдение, может быть в одном из двух состояний: H1 - {функционирует}, H2 -       { не  функционирует}. Априорные вероятности этих состояний P(H1 ) = 0.7, P(H2 ) = 0.3. Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта; первый источник сообщает, что объект не функционирует, второй , что функционирует. Первый источник дает правильные сведения с вероятностью 0,9, а с вероятностью 0,1, что ошибочные. Второй источник менее надежен: он дает правильные сведения с вероятностью 0,7, а с вероятностью 0,3 – ошибочные. На основе анализа донесений найти новые вероятности гипотез.

Решение.

Обозначим А событие, которое наблюдено. А = { Первый источник сообщил H2 , второй - H1 }. 

Условные вероятности этого события при гипотезах H1 и H2 равны P(А / H1 ) = Р (первый источник дал неверные сведения, второй – верные ) = ,
P(А / H2 ) = Р (первый источник дал верные сведения, второй – неверные ) = .

По формуле Байеса находим

.

Таким образом, в результате анализа стала значительно более вероятной вторая гипотеза: объект не функционирует.

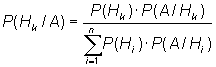Top of page

Home page Home page