| Темы | Следующий пункт | Литература |
|
|
 Вероятность
сложных
событий
Вероятность
сложных
событий
|
|
13.2.1 Условные вероятности Пусть А и В некоторые события в вероятностном пространстве. Сложное событие может представлять собой объединение, пересечение, дополнение и. т. п. простых событий. Получим соотношения, связывающие вероятность сложного события с вероятностями составляющих его простых событий. При анализе того или иного явления перед исследователем часто встает вопрос о том, как влияет на возможность осуществления некоторого события А наступление некоторого другого события В. В теории вероятностей характеристикой связи событий А и В служит так называемая условная вероятность Р(А/В) события А при условии наступления события В, определяемая формулой
В случае эксперимента с
конечным числом N равновероятных
элементарных исходов, пусть N(B) – число элементарных исходов,
приводящих к наступлению события В, а
N(AB) – число элементарных исходов,
приводящих к осуществлению и события А
и события В. Тогда
Условные вероятности обладают всеми свойствами, присущими обычным (безусловным) вероятностям: 1).2). Если наступление события В исключает
возможность осуществления А (
3) Если событие В ведет к обязательному
осуществлению события А (
4) Если событие А есть объединение
непересекающихся событий Поскольку
Р(АВ)
= Р(А)Р(В/А) = Р(В)Р(А/В).
Правило. Вероятность
пересечения событий А и В равна
произведению вероятности одного из
этих событий на условную вероятность
другого события при предположении, что
первое событие произошло. Это правило
называют иногда принципом умножения
вероятностей. Пример
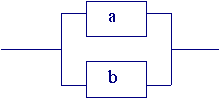
На рисунке показана цепь,
ток в которой может прерваться при
выходе из строя и элемента «а» и
элемента «b». Пусть событие А – выход из строя
элемента «а», а В – выход из строя
элемента «b».
Известно, что вероятности событий А и В
равны: Р(А) = 0,01, Р(В) = 0,02. При выходе из
строя элемента «а» условия работы
элемента «b»
более тяжелые и поэтому Р(В/А) = 0,1. Найти
вероятность Р(А/В) выхода из строя
элемента «а» при условии, что элемент «b»
неисправен. Из правила умножения вероятностей
имеем
Р(АВ) = Р(А)Р(В/А)
= 0,01*0,1=0,001.
Условную вероятность события А/В
находим по формуле |
|
|
|
|