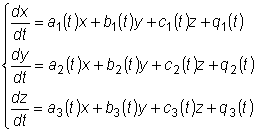Темы | Предыдущий пункт |
Следующий пункт |
Литература
|
|
|

Системы дифференциальных уравнений
|
| |||
|
6.3.1. Системы линейных дифференциальных уравнений |
|
Для изучения свойств систем дифференциальных уравнений ограничимся рассмотрением системы трех уравнений первого порядка с тремя неизвестными функциями. Рассмотрим однородную систему
где функции
Решения системы обладают следующими легко проверяемыми свойствами:
Для неоднородной системы линейных уравнений
общее решение равно сумме общего решения соответствующей однородной системы и какого-либо частного решения неоднородной системы. В дальнейшем будем рассматривать системы линейных дифференциальных уравнений с постоянными коэффициентами. Основные способы решения таких систем: 1) сведение системы к одному дифференциальному уравнению порядка совпадающего с числом неизвестных в системе уравнений; 2) решение систем дифференциальных уравнений с помощью характеристического уравнения.
|
|
|
|
|
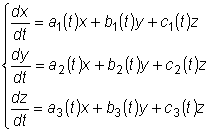 ,
,
 предполагаются непрерывными.
предполагаются непрерывными.
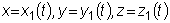 - частное решение системы, то функции
- частное решение системы, то функции
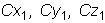 ,
, и
и
 ,
то и функции
,
то и функции 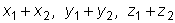 также являются решениями;
также являются решениями;
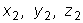 и
и
 системы (2), то функции
системы (2), то функции
 при любых постоянных
при любых постоянных
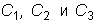 образуют решение.
образуют решение.