Нормальная система уравнений, как правило, может быть заменена одним дифференциальным уравнением, порядок которого равен порядку системы.

Пример

Найти общее решение системы уравнений
.
Продифференцировав первое уравнение по t , заменим производную dy/dt ее выражением из второго уравнения: .
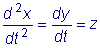Продифференцировав полученное уравнение еще раз, заменим производную dz/dt ее выражением из третьего уравнения:
.
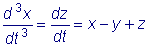Подставляя в последнее уравнение
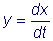и ,
окончательно получим
.
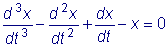Решим это уравнение. Соответствующее ему характеристическое уравнение
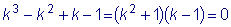
имеет корни .
Следовательно,
.
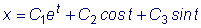Функции y и z в соответствии с соотношениям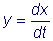и
и
после дифференцирования полученного для x выражения имеют вид:

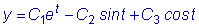
и
.

Нахождение корней характеристического уравнения с использованием системы MathServ

       Характеристическое уравнение:  
       

Замечание

Сводя систему линейных уравнений к одному уравнению высшего порядка, мы всегда получим линейное дифференциальное уравнение. При этом, если исходная система была однородной, то и полученное уравнение высшего порядка будет однородным; в то же время неоднородная система может привести как к неоднородному, так и к однородному уравнению.