С системами дифференциальных уравнений встречаются при изучении
процессов, для описания которых одной функции недостаточно.
Системой дифференциальных уравнений называется
совокупность уравнений, в каждое из которых входит независимая
переменная, искомые функции и их производные.
Решение системы, состоящей из нескольких уравнений с таким же числом
неизвестных функций, можно привести к решению дифференциального
уравнения с одной неизвестной функцией. Метод такого приведения мы
выясним для следующего частного случая.
Пусть нам дана система двух линейных дифференциальных уравнений первого
порядка с двумя неизвестными функциями:
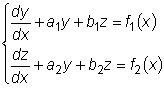 .
.
Для того, чтобы привести решение этой системы к решению одного уравнения
с одной неизвестной функцией, нужно исключить из этой системы одну из
неизвестных функций и ее производную. Пусть, например, мы хотим
исключить z и его производную из двух имеющихся у нас уравнений.
Очевидно, что в данной ситуации мы не сможем одновременно исключить
z и 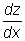 .
Следовательно, нам необходимо иметь по крайней мере еще одно уравнение.
Мы можем получить это дополнительное уравнение, продифференцировав
первое уравнение системы:
.
Следовательно, нам необходимо иметь по крайней мере еще одно уравнение.
Мы можем получить это дополнительное уравнение, продифференцировав
первое уравнение системы:
 .
.
Теперь у нас имеется три уравнения, мы можем исключить из них z и
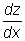 и получим одно уравнение, в которое войдут неизвестная функция y
и производная от этой функции. Это уравнение будет линейным
дифференциальным уравнением второго порядка. Не трудно понять, что, желая
исключить z и его производные, мы должны были дифференцировать
первое уравнение, входящее в систему, а не второе, т.к. в противном
случае в новое, полученное нами дифференциальное уравнение, входила бы
производная
и получим одно уравнение, в которое войдут неизвестная функция y
и производная от этой функции. Это уравнение будет линейным
дифференциальным уравнением второго порядка. Не трудно понять, что, желая
исключить z и его производные, мы должны были дифференцировать
первое уравнение, входящее в систему, а не второе, т.к. в противном
случае в новое, полученное нами дифференциальное уравнение, входила бы
производная  , так что из
системы трех уравнений мы должны были бы исключить величины z,
, так что из
системы трех уравнений мы должны были бы исключить величины z,
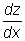 ,
,
 , что невозможно.
, что невозможно.
Получив выражение для y , можно отыскать другую неизвестную
функцию z , подставив выражение для y и его производных
 в первое уравнение данной системы.
в первое уравнение данной системы.

Пример
Пусть дана система
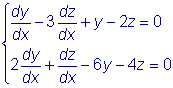 .
.
Приведем эту систему к виду, указанному выше, т.е. добьемся того,
чтобы в одно уравнение входила лишь производная dy/dx,
а в другое лишь производная dz/dx. Умножим второе уравнение на три и
сложим его с первым уравнением, тогда получим:
 .
.
Умножив первое уравнение на два и вычтя его затем из второго уравнения,
получим:
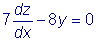 .
.
Решим полученную систему:
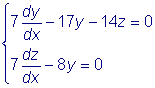 .
.
Продифференцировав первое
из этих уравнений, получаем:
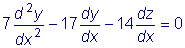 .
.
Подставив в это уравнение значение dz/dx
из второго уравнения нашей системы, получаем:
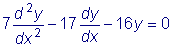 .
.
Решаем это уравнение известным нам методом:
 ;
;
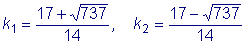 ;
;
 .
.
Подставив выражение для y и dy/dx
в первое из уравнение нашей системы, получим следующее выражение
для z :
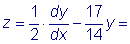
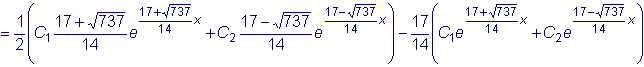
или окончательно
 .
.

Нахождение корней характеристического уравнения
с использованием системы MathServ
Далее несколько усложним задачу, условимся обозначать независимую
переменную буквой t , а неизвестные функции - соответственно
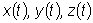 или же
или же
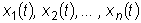 .
.
Число независимых функций обычно равно числу уравнений. Это число
называется порядком системы. Чаще всего приходится иметь дело с так
называемыми нормальными системами.
Нормальной системой дифференциальных уравнений называется
система уравнений вида

Нормальная система уравнений может быть заменена неоднородным
дифференциальным уравнением, порядок которого равен порядку системы.
На этом свойстве нормальных систем основан один из способов их решения,
который будет рассмотрен ниже.
Общее решение системы (1) имеет вид
 ,
,
где 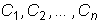 - произвольные постоянные.
- произвольные постоянные.
Чтобы из общего решения системы выделить некоторое частное решение,
задаются начальные условия
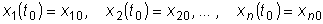 .
Если начальные условия подставить в общее решение, получится система
алгебраических уравнений для определения произвольных постоянных
.
Если начальные условия подставить в общее решение, получится система
алгебраических уравнений для определения произвольных постоянных
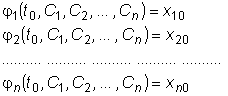 .
.
Частное решение системы, полученное из общего решения при найденных
значениях произвольных постоянных, будет удовлетворять заданным
начальным условиям.

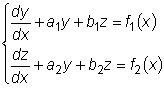 .
. 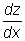 .
Следовательно, нам необходимо иметь по крайней мере еще одно уравнение.
Мы можем получить это дополнительное уравнение, продифференцировав
первое уравнение системы:
.
Следовательно, нам необходимо иметь по крайней мере еще одно уравнение.
Мы можем получить это дополнительное уравнение, продифференцировав
первое уравнение системы:  .
. , так что из
системы трех уравнений мы должны были бы исключить величины z,
, так что из
системы трех уравнений мы должны были бы исключить величины z,
 в первое уравнение данной системы.
в первое уравнение данной системы.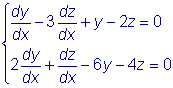 .
.
 .
. 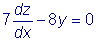 .
.
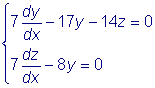 .
.
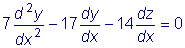 .
.
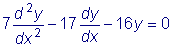 .
.
 ;
;
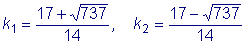 ;
;  .
. 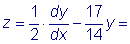
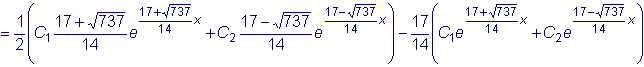
 .
.
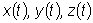 или же
или же
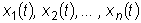 .
.
 ,
, 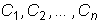 - произвольные постоянные.
- произвольные постоянные.
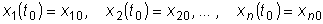 .
Если начальные условия подставить в общее решение, получится система
алгебраических уравнений для определения произвольных постоянных
.
Если начальные условия подставить в общее решение, получится система
алгебраических уравнений для определения произвольных постоянных 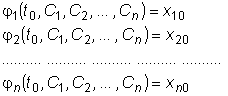 .
.