| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения первого порядка |
|
|
|
|
|
6.1.1. Уравнения с разделяющимися переменными |
Рассмотрим уравнение первого порядка, разрешенное относительно
производной:
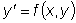 или или
 . .
Это уравнение можно переписать так: 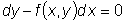 или в более простой форме или в более простой форме
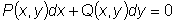 , дающей соотношение между переменными
x и y и их дифференциалами. , дающей соотношение между переменными
x и y и их дифференциалами.
Если в этом уравнении функция P зависит только от x , а функция Q - только от y, то уравнение называется уравнением с разделенными переменными. Таким образом, уравнением с разделенными переменными называется уравнение вида
Решение такого уравнения получается прямым интегрированием. Так как слева
стоит сумма дифференциалов двух функций, которая равна нулю, то сумма их
интегралов равняется постоянной
Пример
Уравнение
Это уравнение может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на выражение
Общий интеграл полученного уравнения имеет вид:
Пример
Дано уравнение В результате вычисления получим: Таким образом, общий интеграл данного уравнения будет иметь вид
|
|
|
|
|
 .
.
 .
.
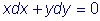 - уравнение с разделенными переменными. Интегрируя, получим общий интеграл:
- уравнение с разделенными переменными. Интегрируя, получим общий интеграл:
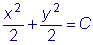 .
. 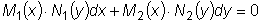 называется уравнением с разделяющимися переменными.
называется уравнением с разделяющимися переменными.

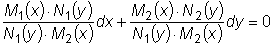
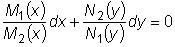 .
.
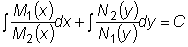 .
.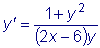 или
или
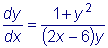 .
. и интегрируем
и интегрируем
 .
.
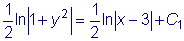 .
. 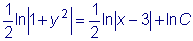 ,
,  .
.