| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения первого порядка |
|
|
|
|
|
6.1.2. Однородные уравнения первого порядка |
|
Рассмотрим сначала понятие однородной функции двух переменных. Пример
Функция
С понятием однородной функции связано понятие однородного
дифференциального уравнения. Первое определение
Уравнение
Для однородного уравнения имеем:
Полагая в последних равенствах
и далее
Для разделения переменных введем новую переменную v = y/x или y = vx. Так как в этом случае dy = xdv +vdx, то последнее уравнение принимает вид: M(1,v)dx + N(1,v)(xdv + vdx) = 0, или [M(1,v) + vN(1,v)]dx +xN(1,v)dv = 0.
Последнее уравнение является уравнением с разделяющимися переменными
x и v , из него определяется v , а затем
искомая функция y = vx. Второе определение Если уравнение может приведено к виду: dy/dx = F(x,y) = F(v), где v = y/x, то оно называется однородным дифференциальным уравнением первого порядка. Для приведения его к уравнению с разделяющимися переменными
используется подстановка
Пример
Решить уравнение (y 2 - 3x 2)dx + 2xydy = 0,
при начальном условии: y(0) = 0 .
Здесь M(x,y) = (y 2 - 3x 2)
и N(x,y) = 2xy - однородные функции измерения 2.
Применим подстановку y = vx, при этом dy = xdv +vdx.
Получим:
x 2(v 2 - 3)dx + 2x 2v(xdv +vdx) = 0.
После интегрирования получим:
x 3(v 2 - 1) = C или
общий интеграл:
x(y 2 - x 2) = C
Используя начальные условия y(0) = 0
имеем
0(0 2 - 0 2) = C , отсюда C = 0.
Частное решение данного уравнения: x(y 2 - x 2) = 0
или
x = y и x = - y
|
|
|
|
|
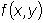 называется однородной функцией измерения n,
если при любом t справедливо тождество
f (tx, ty) = t n f(x, y) .
называется однородной функцией измерения n,
если при любом t справедливо тождество
f (tx, ty) = t n f(x, y) .
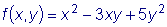 есть однородная функция измерения 2, т.к.
есть однородная функция измерения 2, т.к.
 .
. (1)
(1)
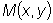 и
и
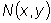 являются однородными функциями одного и того же измерения.
являются однородными функциями одного и того же измерения.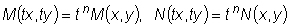 .
.
 , получаем
, получаем
 .
.
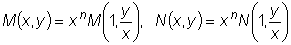

 .
.
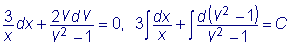 .
.