| Темы | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения первого порядка |
|
|
|
|
|
Дифференциальным уравнением называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную искомой функции. Символически дифференциальное уравнение можно написать так
или
Неизвестной здесь является функция y, входящая под знак производных (или дифференциалов). Если искомая функция y(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным. В этой главе мы будем рассматривать только обыкновенные дифференциальные уравнения. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, уравнение Решением дифференциального уравнения называется всякая функция y(x), которая будучи подставленной в уравнение, обращает его в тождество. Решение еще называется интегралом дифференциального уравнения. Пример
Рассмотрим уравнение
Функция
Действительно,
Заметим, что рассматриваемое уравнение имеет бесчисленное множество решений вида:
Решение дифференциальных уравнений первого порядка
Дифференциальным уравнением первого порядка
называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную первого порядка искомой функции.
Дифференциальное уравнение первого порядка имеет вид
Общее и частное решение
Общим решением дифференциального уравнения первого порядка называется решение
Равенство вида
Пример
Рассмотрим уравнение
Общим решением этого уравнения является семейство функций
Действительно, при любом значении C эта функция удовлетворяет уравнению:
Это решение можно получить, используя нижеприведенный апплет для
построения поля направлений и интегральных кривых для уравнения
первого порядка.
Интегральные кривые
С геометрической точки зрения общее решение уравнения первого порядка
представляет собой семейство кривых на плоскости xOy, зависящее
от одной произвольной постоянной C.
Эти кривые называются интегральными кривыми данного
дифференциального уравнения. Решить или проинтегрировать данное дифференциальное уравнение
это значит:
а) найти его общее решение или общий интеграл, если не заданы начальные условия,
или
б) найти частное решение, удовлетворяющее заданным начальным условиям. | |
|
|
|
|
Геометрическая интерпретация дифференциального уравнения первого порядка |
|
|
Пусть дано дифференциальное уравнение, разрешенное
относительно производной:
Пример
Рассмотрим уравнение
Теорема существования и единственности решения дифференциального
уравнения.
Рассматривая уравнение первого порядка
Теорема. | |
|
|
|
|

 .
.

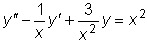
 .
.
 является решением этого уравнения.
является решением этого уравнения.

 .
.

 ,
где
,
где
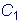 и
и
 -
произвольные постоянные.
-
произвольные постоянные.

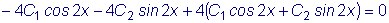 .
.
 .
.
 ,
зависящее от одной произвольной постоянной C, придавая конкретное значение которой
,
зависящее от одной произвольной постоянной C, придавая конкретное значение которой
 ,
можно получить решение
,
можно получить решение
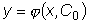 ,
удовлетворяющее любому заданному начальному условию
,
удовлетворяющее любому заданному начальному условию
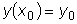 .
.
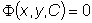 ,
неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
,
неявно задающее общее решение, называется общим интегралом дифференциального уравнения.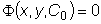 называется в этом случае частным интегралом.
называется в этом случае частным интегралом.
 .
.
 .
.
 .
.
 .
.
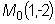 Заметим, что задать начальное условие для уравнения первого порядка с
геометрической точки зрения означает задать точку
Заметим, что задать начальное условие для уравнения первого порядка с
геометрической точки зрения означает задать точку
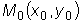 , через которую должна пройти соответствующая интегральная кривая.
, через которую должна пройти соответствующая интегральная кривая.
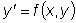 .
.  определяет значение
производной
определяет значение
производной
 , т.е. определяет угловой
коэффициент касательной к интегральной кривой, проходящей через эту
точку.
, т.е. определяет угловой
коэффициент касательной к интегральной кривой, проходящей через эту
точку.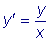 .
.
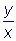 , т.е. совпадает с угловым
коэффициентом прямой, проходящей через начало координат и точку
с координатами (x,y).
Очевидно, что интегральными кривыми будут прямые y=Cx,
где C - произвольная постоянная, т.к. направление этих прямых
всюду совпадает с направлением поля.
, т.е. совпадает с угловым
коэффициентом прямой, проходящей через начало координат и точку
с координатами (x,y).
Очевидно, что интегральными кривыми будут прямые y=Cx,
где C - произвольная постоянная, т.к. направление этих прямых
всюду совпадает с направлением поля. 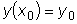 частного решения,
удовлетворяющего этому условию.
частного решения,
удовлетворяющего этому условию. 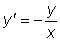 .
.  , а интегральными
кривыми - семейство гипербол, причем через каждую точку
, а интегральными
кривыми - семейство гипербол, причем через каждую точку
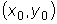 , не лежащую на оси Oy
проходит одна и только одна интегральная кривая, т.е. рассматриваемое
уравнение имеет единственное решение, проходящее через точку, не лежащую
на оси Oy, но оно не имеет решения, проходящего через точку,
взятую на оси Oy.
, не лежащую на оси Oy
проходит одна и только одна интегральная кривая, т.е. рассматриваемое
уравнение имеет единственное решение, проходящее через точку, не лежащую
на оси Oy, но оно не имеет решения, проходящего через точку,
взятую на оси Oy. 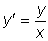
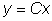 является общим решением
этого уравнения, а при любом значении C прямая
является общим решением
этого уравнения, а при любом значении C прямая
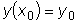 , отвечает следующая
теорема.
, отвечает следующая
теорема.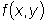 и ее частная производная
и ее частная производная
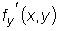 непрерывны в некоторой области D на плоскости xOy .
Тогда, если точка
непрерывны в некоторой области D на плоскости xOy .
Тогда, если точка
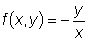
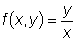
 и,
следовательно, не являются непрерывными. Это обстоятельство и привело,
в первом случае, к отсутствию решений, проходящих через точки оси Ox ,
во втором - к нарушению единственности в точке (0,0).
и,
следовательно, не являются непрерывными. Это обстоятельство и привело,
в первом случае, к отсутствию решений, проходящих через точки оси Ox ,
во втором - к нарушению единственности в точке (0,0).