| Темы | Предыдущий пункт | Следующий пункт |Литература |
|
|

Векторная алгебра |
|
1.2.10 Арифметическое n - мерное векторное пространство.
Решая систему
линейных уравнений методом Гаусса, мы оперируем по существу не с самими
уравнениями
Назовем любую систему чисел, заданных в определенном порядке
арифметическим n-мерным
вектором. Числа Два вектора одной и той же размерности
считаем равными и
обозначаем
Суммой двух векторов
Произведением
вектора
Легко проверить, что эти операции обладают переместительным, сочетательным и распределительным свойствами:
Вектор, все
координаты которого равны нулю, называется нулевым вектором и
обозначается При исследовании
какого-либо процесса обычно приходится иметь дело не с одним вектором, а
с целым множеством или системой векторов (одной и той же размерности):
Выражение вида
Пример 1. Найти линейную
комбинацию Решение: Используя свойства (4) и (5) получим:
Если вектор
Для того, чтобы
охарактеризовать взаимное расположение векторов, вводится понятие
линейной зависимости системы векторов, согласно которому система
векторов
Для двух векторов свойство линейной зависимости означает их коллинеарность, для трех векторов - компланарность.
Пример 2. Дана система
векторов
Решение: На основании
определения линейной зависимости запишем соотношение
общее решение
которой
Система векторов
оказывается связанной линейной зависимостью
Можно показать, что
в пространстве
Такая система векторов называется базисом. Если координаты данной системы векторов записать в виде матрицы, то введенное ранее понятие ранга матрицы будет указывать максимальное число линейно-независимых векторов в данной системе.
Пример 3. Для системы векторов:
найти базис и выразить через него все остальные векторы системы. Решение: Составляем из координат векторов матрицу и преобразуем ее по схеме Гаусса:
Ранг матрицы А
равен 3, следовательно, базис исходной системы векторов состоит из трех
векторов, а, именно,
С каждой системой линейных уравнений
можно связать систему векторов
Тогда система
линейных уравнений эквивалентна одному векторному уравнению
Например, для
системы
Векторная запись
позволяет по-новому взглянуть на вопрос о совместности системы линейных
уравнений, который может быть сформулирован в следующем виде: допускает
ли вектор разложение по векторам
|
|
|
|
|
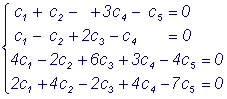 ,
,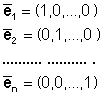

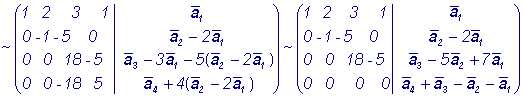 .
.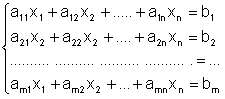
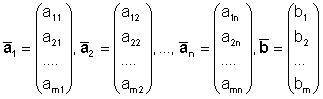 .
.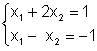 векторная запись будет
векторная запись будет