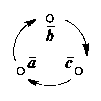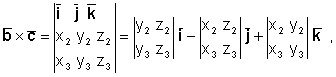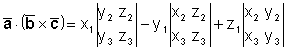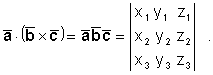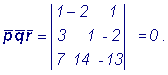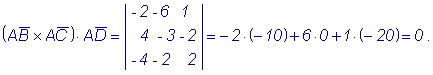Во - первых, можно перемножать два вектора и скалярно и полученный скаляр умножить на третий вектор . В результате получается вектор, называемый простейшим произведением трех векторов: .

Во - вторых, можно перемножать два вектора и  векторно и полученный вектор умножить тоже векторно на третий вектор . В результате получается вектор, называемый векторно - векторным или двойным векторным произведением трех векторов: .

Из этих произведений наибольший практический интерес имеет смешанное произведение, которое мы и рассмотрим подробнее.

Векторно - скалярным или смешанным произведением трех векторов называется произведение, которое получается скалярным  умножением векторного произведения двух векторов на третий вектор, т.е. произведение вида .

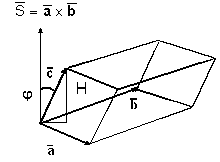
Смешанное произведение представляет собой скаляр, выясним его геометрический смысл. Обозначим , тогда

(*).

Чтобы истолковать полученный результат, мы построим на векторах , , параллелепипед, основанием которого будем считать параллелограмм со сторонами , . Площадь этого основания: . Обозначим через H высоту, опущенную на это основание. Тогда объем V параллелепипеда определится известной формулой .

Теперь нам придется различить два случая. В первом случае, когда перемножаемые векторы , , образуют правую тройку (рис.2.18), т.е. когда из конца третьего вектора поворот от первого вектора ко второму виден происходящим против хода часовой стрелки, и формула (*) примет вид .

Таким образом, векторно-скалярное произведение трех векторов, образующих правую систему, равно объему параллелепипеда, построенного на этих векторах. Во втором случае, когда перемножаемые векторы , , образуют левую систему (т.е. когда с конца  третьего вектора поворот от первого вектора ко второму виден происходящим по ходу часовой стрелки, и формула (*) примет вид .

Если мы имеем дело с векторно-скалярным произведением трех векторов, образующих левую систему, то его величина отличается только  знаком от объема параллелепипеда, построенного на  перемножаемых векторах.

Итак, , причем знак "+" получается, когда перемножаемые векторы образуют правую систему, и знак "-", когда их система левая.

Отсюда следует, что объем параллелепипеда, построенного на трех векторах, всегда равен абсолютной величине их векторно-скалярного произведения:

Законы векторно-скалярного умножения

1) Закон сочетательности ;

Учитывая закон сочетательности, векторно - скалярное произведение трех векторов  обозначают условно так: или .

2) Закон круговой переместительности

.

Видим, что при перестановке множителей не нарушающей их кругового порядка, векторно-скалярное произведение не меняется, при перестановке же множителей, нарушающей круговой порядок,  векторно-скалярное произведение меняет только свой знак. Правило легко запомнить, используя схему, приведенную на рис. 2.19.

3) Закон распределительности .

4) Закон сочетательности относительно скалярных множителей: .

Векторно-скалярное произведение трех векторов равно нулю тогда и только тогда, когда перемножаемые векторы компланарны. Действительно, объем параллелепипеда, построенного на компланарных векторах, равен нулю, и наоборот, если объем равен нулю, то векторы компланарны.

В частности, векторно-скалярное произведение равно нулю, если в нем два множителя одинаковы: , например.

Векторно-скалярное произведение можно записать в координатной форме.

Пусть векторы , , разложены по ортам

Тогда, согласно (2.8), получим

следовательно

или, окончательно,

(2.10)

Пример 1.