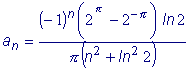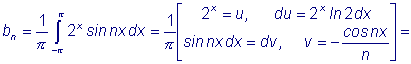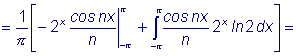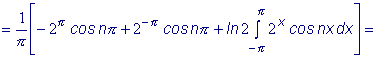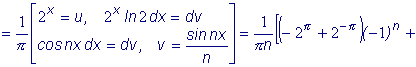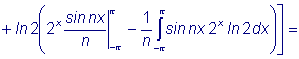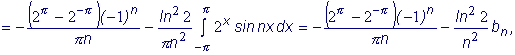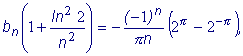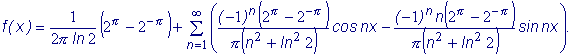| Темы | Предыдущая лекция |Следующий пункт | Литература | ||||
|
|
||||

Ряды Фурье. |
||||
|
|
||||
|
Функциональный ряд вида:
где коэффициенты ряда вычисляются по формулам:
Называется рядом Фурье для периодической функции периода T = 2l, заданной на отрезке [- l, l ]. Согласно теореме Дирихле функция f(x) может быть разложена в ряд Фурье, если 1. f(x) непрерывна или имеет конечное число точек разрыва 1 рода; 2. f(x) имеет конечное число экстремумов. Тогда ряд Фурье функции f(x) сходится на всем отрезке [- l, l ] и сумма ряда S(x) равна: 1. S(x) = f(x) во всех точках непрерывности, лежащих внутри промежутка ( -l, l ); 2. 3.
Пример: Разложить в ряд Фурье функцию f(x) =
2x на отрезке [- Решение: Найдем коэффициенты ряда , заменив в формулах
(2) l на
Аналогично:
Следовательно, подставляя полученные коэффициенты в формулу (1) найдем разложение данной функции в ряд Фурье:
На границах промежутка Функция | ||||
|
|
||||
|
|
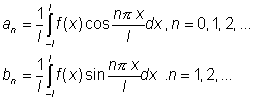
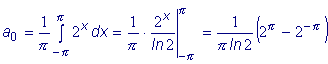
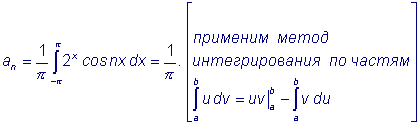
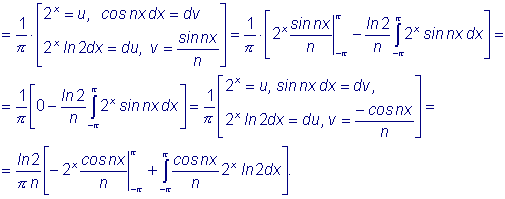
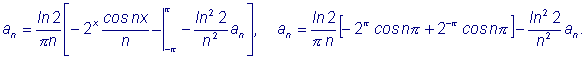
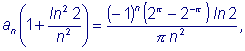 так как cos πn
=(-1)n,
так как cos πn
=(-1)n,