| Темы | Предыдущая лекция | Следующий пункт | Литература | ||||||||||||||
|
|
||||||||||||||

Степенные ряды |
||||||||||||||
|
|
||||||||||||||
|
11.2.1. Функциональные и степенные ряды
|
||||||||||||||
Пусть
функции Ui (x) (i=1, 2, 3, ... n,...) определены в области Dx . Тогда выражение вида
называется функциональным рядом. Он называется
сходящимся в точке x = x0
если сходится числовой ряд Множество значений при которых ряд
(1) сходится,
называется областью сходимости функционального
ряда. Обозначим ее Ds.
Как правило, область не совпадает с
областью Dx,
а является ее частью
Пример Найти область сходимости функционального ряда
Данный ряд является суммой членов
геометрической прогрессии со
знаменателем q
= ln x. Такой ряд сходится, если
Пусть S(x) сумма ряда (1), а Sn(x) = U1(x) + U2(x) + ... + Un(x) n - я частичная сумма ряда, то ее n - й остаток определяется равенством: rn (x) = S (x) - Sn (x) = Un+1 (x) + Un+2 (x) +...
В области сходимости ряда: Приведем другое определение суммы функционального ряда: Функция
S(x) называется
суммой ряда (1) в некоторой области
D,
если для любого
В общем случае
N0 зависит от х, т.е. при заданном В случае равномерной сходимости функционального ряда его
n - я частичная сумма является приближением суммы ряда с одной и той же точностью
для всех Функциональный ряд (1) называется мажорируемым в некоторой области D, если существует сходящийся числовой ряд:
Такой, что для
всех Ряд (3) называется мажорантным (мажорирующим) рядом. Например, функциональный ряд:
мажорируется рядом: Данный функциональный ряд равномерно сходится на всей оси ОX, поскольку он мажорируется при любом x. Равномерно сходящиеся ряды обладают некоторыми общими свойствами: 1) Если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке; 2) Если члены ряда
(1) непрерывны на
отрезке
где S(x)– сумма ряда (1);
3) Если ряд (1), составленный из
функций, имеющих непрерывные
производные на отрезке [a, b],
сходится на этом отрезке к сумме
S(x) и ряд
Степенные ряды. Степенным рядом называется функциональный ряд
вида
Теорема Абеля. 1. Если степенной ряд (4) сходится при некотором значении
2. Если степенной ряд (4) расходится
при некотором значении x = x2
, то он расходится при любых x для которых
Неотрицательное
число R, такое, что при всех Интервал (- R ; R ) называется интервалом сходимости ряда (4). Радиус сходимости степенного ряда (4) определяется формулой:
если, начиная с некоторого
Пример: Найти область сходимости степенного ряда:
Так как На концах этого интервала ряд может сходиться или расходиться.
При x = - 3 / 2 данный ряд
принимает вид:
Если дан ряд вида
Пример: Найти
область сходимости степенного ряда: Найдем радиус сходимости данного ряда:
На всяком отрезке
Пример: Найти сумму ряда:
При
Так как
| ||||||||||||||
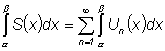
 или
или 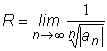
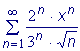
 ,
,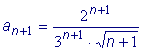 , то
, то 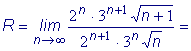
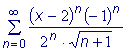
 ,
т.е. ряд сходится в интервале (0; 4). При x = 0 получаем ряд
,
т.е. ряд сходится в интервале (0; 4). При x = 0 получаем ряд 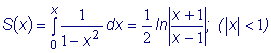 .
.