| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Числовые ряды |
|
|
|
|
|
11.1.5. Абсолютная и условная сходимость рядов. Признак Даламбера. |
||||||||||
|
Введем два понятия.
Ряд
называется абсолютно сходящимся, если сходится ряд
образованный из абсолютных значений членов ряда (1). Очевидно, что при сходимости ряда (2) ряд (1) не может быть расходящимся, т.к. удовлетворяет ряд (2), то удовлетворяет и ряд
(1).
Таким образом, когда ряд (2) сходится,
тогда сходится и ряд (1), причем в
этом случае ряд (1) Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
| ||||||||||
|
Признак Даламбера |
||||||||||
|
Пользуясь принципом сравнения рядов, можно получить простой признак абсолютной сходимости ряда. Пусть для ряда
выполнено условие :
при всех n, начиная с некоторого номера n0. Докажем, что ряд (1) сходится абсолютно. Действительно, в силу условия (2) имеем
Отсюда получим: .
Так
как ряд
Отсюда в свою очередь вытекает сходимость ряда
для которого ряд (4) является остаточным членом. Но сходимость ряда (5) и означает абсолютную сходимость данного ряда (1). Заметим, что если для ряда (1) условие (2) для него выполнено, а значит, ряд (1) сходится абсолютно. Действительно, если возьмем некоторое число q,
удовлетворяющее условию k < q
< 1, то при достаточно
большом nо
для всех 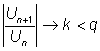 , когда , когда Если же для ряда (1)
окажется, что то при достаточно большом nо
для всех Если же нужно
дополнительное исследование.
Все
сказанное доказывает справедливость
утверждения, называемого признаком
Даламбера
сходимости
ряда: Если
для ряда U1 + U2 + U3 + ... +Un +... имеем:
то при k<1
ряд сходится
абсолютно, а при k
>1 ряд расходится. Если k =1, то вопрос о сходимости
ряда нужно решать
другими
средствами.
Пользуясь признаком Даламбера, исследовать на сходимость ряд ы:1) Решение:
Найдем
2) Решение:
3) Решение:
4) Решение:
|
|
|
|
|
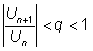
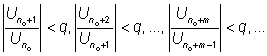
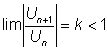 ,
то
,
то
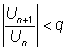
 ,
,
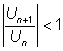 или
или 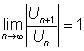 , то ряд (1) может оказаться как
сходящимся, так и расходящимся,
, то ряд (1) может оказаться как
сходящимся, так и расходящимся,
 ,
,
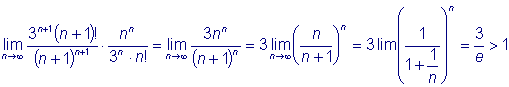
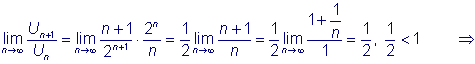 ряд сходится.
ряд сходится.

 - ряд сходится.
- ряд сходится.