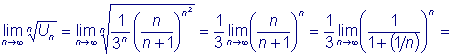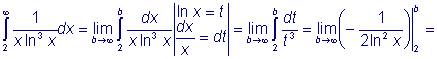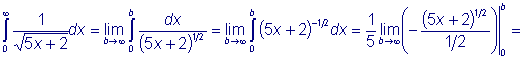Темы | Предыдущий пункт | Следующий пункт | Литература
Лекция 11.1.

Числовые ряды

11.1.6. Радикальный признак Коши. Интегральный признак Коши сходимости рядов.

 

Радикальный признак Коши.

Если для ряда с положительными членами существует , то этот ряд сходится при l >1,  расходится при l >1.  Если l =1, то вопрос о сходимости  ряда остается открытым.

Примеры:

Пользуясь признаком Коши исследовать на сходимость ряды:

1)             Найдем для данного ряда:

, следовательно, ряд сходится.

2)     Найдем:

 

, следовательно, ряд сходится.

Интегральный признак Коши сходимости рядов.

 

 Пусть члены ряда  

U1 + U2 + U3 + ... + Un + ... (1)

положительны и не возрастают, т.е.

 

и пусть f(x) такая непрерывная невозрастающая функция, что 

f(1)=U1, f(2)=U2, ... , f(n)=Un (2)

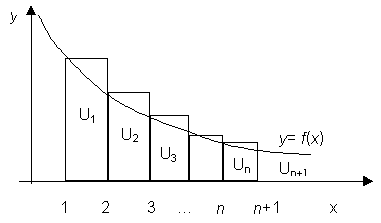
тогда справедливы следующие утверждения:

1) если несобственный интеграл   сходится, то сходится и ряд (1)

2) если несобственный интеграл    расходится, то расходится и ряд (1).

Докажем эти утверждения.

Изобразим члены ряда (1) геометрически, откладывая на оси OX номера  1, 2, ..., n+1,... членов ряда, а по оси OY- соответствующие значения ряда

 

Построим на том же чертеже график непрерывной невозрастающей функции y = f(x), удовлетворяющей условию (2). Площади построенных прямоугольников соответственно равны:   U1, U2 , U3 , ... , Un , ... . Сумма же площадей прямоугольников равна сумме Sn первых n членов ряда (1). С другой стороны, ступенчатая фигура, образованная этими прямоугольниками, заключает область, ограниченную кривой y=f(x) и прямыми x=1, x=n+1,  y=0. Площадь этой области равна  
(3) 

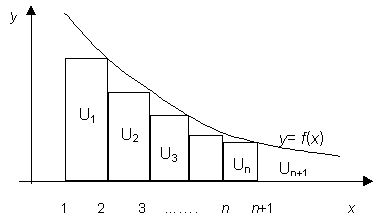
Теперь рассмотрим чертеж.

Здесь первый из построенных прямоугольников имеет площадь U2, второй – U3, последний –

Un+1 . Следовательно, сумма площадей всех прямоугольников равна сумме всех членов ряда (1),

начиная со второго до (n+1) - го, т.е. равна Sn+1 - U1.

С другой стороны, ступенчатая фигура, образованная этими прямоугольниками, содержится

внутри криволинейной трапеции, ограниченной кривой y = f(x) и прямыми x = 1, x = n, y = 0.

Площадь этой фигуры равна .  Следовательно,     или 
(4)

Рассмотрим теперь оба случая.

1. Предположим, что интеграл сходится, т.е. имеет конечное значение. Так как  то в силу неравенства (4):

т.е. частичная сумма Sn  остается ограниченной при всех значениях.  Но при увеличении n она возрастает, так как все члены положительны. Следовательно, Sn при  имеет конечный предел , т.е. ряд сходится.

2. Предположим далее, что .  Это значит, что неограниченно возрастает при возрастании n.  Но тогда в силу неравенства (3) Sn также неограниченно возрастает при возрастании n, т.е. ряд расходится.

Таким образом, утверждения полностью доказаны.

Итак, ряд с положительными убывающими членами  Un = f(x) сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл , где f(x) - непрерывная убывающая функция, нижним пределом интеграла может быть любое положительное число из области определения.

Это утверждение и является интегральным признаком Коши.

Примеры:

Исследовать по интегральному признаку сходимость следующих рядов:

1)    

Решение:

Заменяем в формуле общего члена ряда номер n непрерывной переменной x и убеждаемся, что полученная функция является непрерывной и убывающей во всем бесконечном интервале изменения x. Затем находим несобственный интеграл: 

 Следовательно, несобственный интеграл сходится, и ряд тоже сходится.

2)   

Решение

 

т.е. несобственный интеграл расходится, и ряд тоже расходится.

 Задачи для самостоятельного решения.