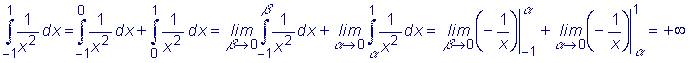Пусть f(x) непрерывна всюду на [a, b] кроме точек c₁ < c₂ < ... < c_n лежащих между a и b. (То есть 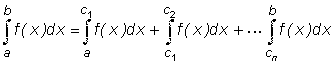при .) Тогда под интегралом от a до b понимается сумма:

Если не учитывать разрывность функции на отрезке интегрирования можно получить ошибочное значение интеграла.

Пример:
Применим формулу Ньютона-Лейбница для интеграла . 

Полученный результат неверен, поскольку функция положительна.
Ошибка получена, так как не учтено, что на отрезке интегрирования [-1, 1] существует особая точка x = 0, в которой функция терпит разрыв второго рода.