| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Неcобственный интеграл. |
|
|
|
|
|
5.3.2. Интегралы от разрывных функций. |
|
Допустим, что отрезок [a, b] - конечен, но функция f(x) не
ограничена на нем, а стремится к бесконечности при приближении к одной из особых точек
c1, c2, ..., cn , которые называются точками разрыва. Рассмотрим сначала одну особую точку Пусть точка 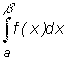 .
Если существует конечный предел .
Если существует конечный предел 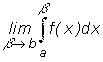 , то несобственнный интеграл от
разрывной функции сходится. в противном случае интеграл расходится. , то несобственнный интеграл от
разрывной функции сходится. в противном случае интеграл расходится.
Примеры: 1.  Интеграл расходится. Интеграл расходится. 2. 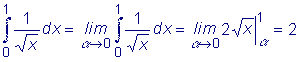 Интеграл сходится. Интеграл сходится.
Если обе точки a и b - особые, то интеграл определяется как сумма: 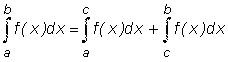 , где a < c < b. , где a < c < b.
|
|
|