| Темы | Предыдущая лекция | Следующий пункт | Литература | ||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||

Приближенное вычисление определенных интегралов. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
5.4.1. Формула трапеций. |
||||||||||||||||||||||||||||||||||||
|
Часть интегралов, как уже было сказано, не имеют первообразных в элементарных функциях,
поэтому для их нахождения применяют приближенные вычисления. В результате построения наша криволинейная трапеция
разбилась на ряд вертикальных полосок одной и той же ширины h, каждую из которых приближенно можно принять за трапецию.
Суммируя площади этих трапеций получим формулу трапеций:
Вычислить приближенно
Находим
и по формуле трапеций имеем Точное значение этого же интеграла, полученное по формуле Ньютона-Лейбница
|
||||||||||||||||||||||||||||||||||||
|
|
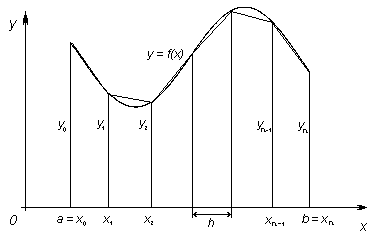
 воспользуемся его
геометрическим смыслом. Как известно такой интеграл представляет собой площадь криволинейной трапеции
ограниченной линией y = f(x), осью Ox и двумя прямыми x = a и x = b (Рис. 1)
воспользуемся его
геометрическим смыслом. Как известно такой интеграл представляет собой площадь криволинейной трапеции
ограниченной линией y = f(x), осью Ox и двумя прямыми x = a и x = b (Рис. 1) 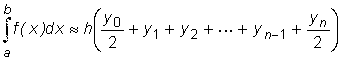

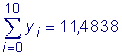 ;
;