| Темы | Предыдущая лекция | Следующий пункт | Литература | |||
|
|
|||

Неcобственный интеграл. |
|||
|
|
|||
|
5.3.1. Интеграл по бесконечному промежутку. |
|||
При определении интеграла  предполагалось, что: предполагалось, что: 1) Промежуток интегрирования [a, b] конечен; 2) Подинтегральная функция f(x) - определена и непрерывна на [a, b]. Иногда от одного или от обоих этих предположений можно отказаться. В этом случае интеграл имеет название несобственный интеграл. Пусть функция f(x) задана и непрерывна на полуинтервале Тогда для
любого x = B существует интеграл Если существует конечный предел
При этом говорят, что интеграл сходится. В противном случае (предел не существует или
равен
Примеры:
Предел не существует. Несобственный интеграл не существует. Несобственный интеграл расходится. Интеграл сходится.
Доказательство: Пусть Рис. 1 Если ввести обозначение | |||
|
|
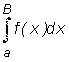 .
.  , то этот предел называют несобственным интегралом
с бесконечным верхним пределом интегрирования функции f(x) на интервале
, то этот предел называют несобственным интегралом
с бесконечным верхним пределом интегрирования функции f(x) на интервале 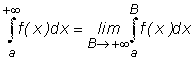


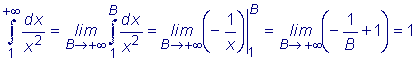
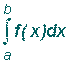 возрастает вместе с
b.
возрастает вместе с
b. 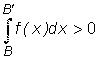 (интеграл от положительной функции),
то
(интеграл от положительной функции),
то 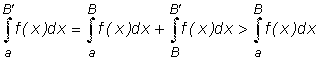
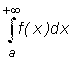 имеет
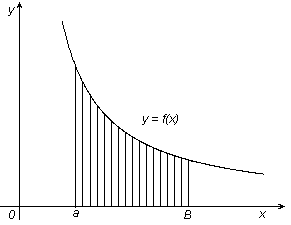
(конечное или бесконечное) числовое значение. Геометрически - это площадь
фигуры, ограниченной слева прямой х = a, снизу осью Ox,
сверху графиком y = f(x) и неограниченно простирающейся прямой направо. (Рис. 1)
имеет
(конечное или бесконечное) числовое значение. Геометрически - это площадь
фигуры, ограниченной слева прямой х = a, снизу осью Ox,
сверху графиком y = f(x) и неограниченно простирающейся прямой направо. (Рис. 1) 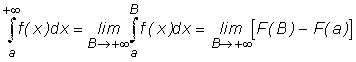 .
.

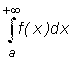 .
.  ;
; 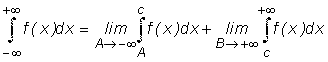 , где
, где