| Темы | Предыдущая лекция | Следующий пункт | Литература | |
|
|
|

Приложения определенного интеграла. |
|
|
|
||||||
|
5.2.1.Вычисление площадей плоских фигур. |
||||||
|
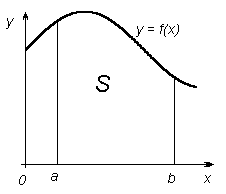
Задача 1. Найти площадь криволинейной трапеции (рис.1),
Ограниченной дугой графика функции y = f(x), отрезком
Рис.1
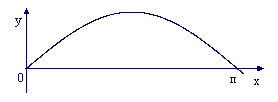
Пример: Вычислить площадь одной волны синусоиды
y = sin x
Искомую площадь можно рассматривать как разность двух криволинейных трапеций.
Вычислить площадь фигуры, ограниченной линиями:
y =3x - x2 и y = -x.
где
Вычислить площадь фигуры, ограниченной эллипсом:
|
||||||
|
|
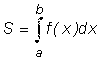
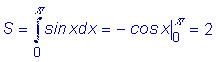
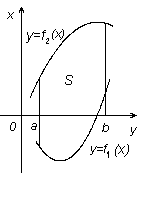
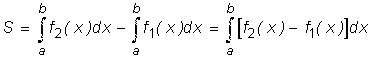
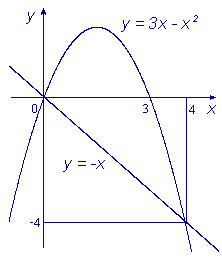
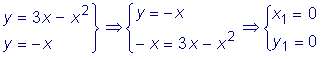 и
и 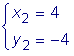
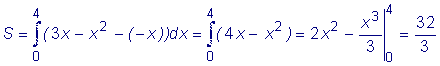 .
. 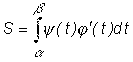
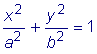 .
.
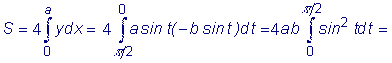
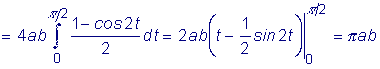 .
.