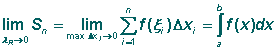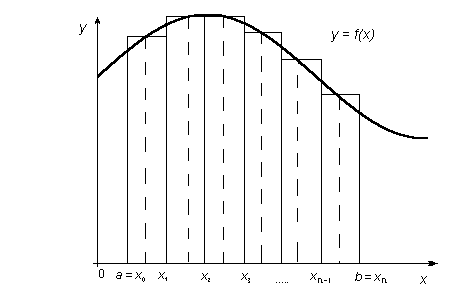
Пусть на отрезке [a, b] определена функция   y = f(x). Отрезок [a, b] разобьем на n частей (разбиение R) точками: a = x₀ x₁ x₂ ... x_n-1 x_n = b.
На любом интервале [x_i , x_{i +1}] выберем по произвольной точке , (Рис.1)
Составим n - ную интегральную сумму функций f(x)  на отрезке [a, b]
; где  

Рис. 1

Геометрический смысл суммы S_n - это и есть алгебраическая сумма площадей прямоугольников, в основании которых лежат отрезки , а высоты равны (В том случае если функция не отрицательна.)

Обозначим через -максимальную длину отрезков [x_i ,x_{i +1}] разбиения R.

Предел (если он существует), к которому стремится интегральная сумма S_n при , называется определённым интегралом от функции f(x) на отрезке [a, b] и обозначается как:

(1)

где а, b - нижний и верхний пределы интегрирования.

Предел (1) называют интегралом Римана и функцию, для которой этот предел существует, называют интегрируемой в смысле Римана.

Данное определение эквивалентно следующему:

Определенным интегралом от функции f (x) на отрезке [a, b] называется число I, удовлетворяющие следующему свойству: для всякого можно найти число  такое, что для любого разбиения R отрезка [a, b], у которого , выполняется равенство:

при произвольном выборе точек

В случае непрерывных функций понятие определенного интеграла введено Коши. Говорят, что непрерывная на [a, b] функция интегрируема в смысле Коши.
Непосредственное вычисление определенного интеграла по формуле (1) связано с рядом трудностей, так как интегральные суммы имеют сложный вид, и найти их предел нелегко.