| Темы | Предыдущая лекция |Следующий пункт | Литература | ||||||||||||||||
|
|
||||||||||||||||
 Прямая
линия в пространстве.
Прямая
линия в пространстве.
|
||||||||||||||||
|
2.4.1 Уравнение прямой линии. Положение прямой линии в
пространстве будет вполне определенно,
если зададим на прямой определенную
точку M0 при помощи ее радиус –
вектора Этот вектор
где t - числовой множитель, и он может принимать любые значения в зависимости от положения точки М на прямой. Следовательно, равенство (1) можно переписать так:
Уравнение (2) называется векторным уравнением прямой линии. От векторного уравнения (2) можно перейти к координатным уравнениям. Обозначим декартовы координаты точки M0 относительно системы координат с началом в точке О через a, b, c , координаты точки М через x, y, z, и координаты вектора
Тогда уравнение (2) в проекциях будет иметь вид:
Уравнения (3) называются параметрическими уравнениями. Из уравнений (3), исключая параметр можно получит уравнения вида:
или
Уравнение (4) называют каноническим уравнением прямой где
то есть геометрически это обозначает перпендикулярность прямой к оси ОХ. Прямую линию можно записать уравнением, представляющем прямую как линию пересечения двух плоскостей. Через каждую прямую проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения двух таких плоскостей, рассматриваемые совместно, представляют собой уравнение прямой, то есть
есть уравнение прямой в пространстве. Уравнение (5) называется общим уравнением прямой. От общих уравнений прямой можно перейти к каноническому уравнению, а затем к параметрическому. Чтобы от уравнений (5) перейти к уравнению (4) надо найти координаты точки, лежащей на прямой. Координаты точки находятся из системы уравнений (5), где выбирается одна из координат произвольно: z = k. После подстановки значения z в систему (5) находим x и y.Для отыскания
и
Пример .
Привести к каноническому и
параметрическому виду уравнение
прямой:
Решение. 1. Пусть a = 2, b = 0, c
= 1. 2. Найдем направляющий вектор
прямой.
Каноническое уравнение
прямой будет:
3. Получим параметрическое уравнение
прямой.
Сравнивая эти два уравнения,
получим
|
|
|
|
|
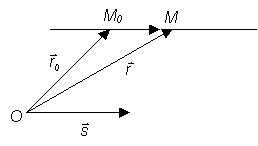 Рис.1.
Рис.1.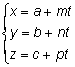
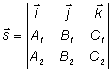
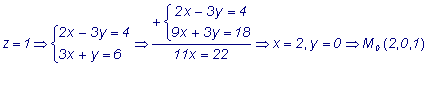 -
точка, принадлежащая прямой и
-
точка, принадлежащая прямой и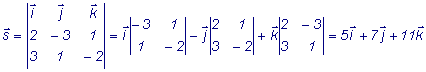 .
.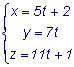 - параметрическое уравнение прямой.
- параметрическое уравнение прямой.