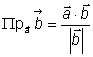| Темы | Предыдущая лекция | Следующий пункт | Литература | ||||||
|
|
||||||
 Плоскость
и виды ее уравнения в пространстве.
Плоскость
и виды ее уравнения в пространстве.
|
||||||
|
2.3.1 Нормальное уравнение плоскости. Положение плоскости в
пространстве будет вполне определенно,
если зададим ее расстояние р от начала
координат О и единичный вектор
Когда точка М движется по
плоскости, то ее радиус – вектор
Это условие имеет место лишь для точек плоскости и нарушается, если точка М лежит вне плоскости. Таким образом, равенство (1) выражает свойство, общее всем точкам плоскости и только им. Используя равенство
Равенство (1) приводим к виду:
Уравнение (2) записано в векторной форме. Переходя к координатам и помещая начало координат в начало векторов, запишем:
Где
где
Уравнение (2) в координатной форме будет иметь вид:
Таким образом, уравнение (3) является нормальным уравнением плоскости в координатной форме и выражает собой условие, когда точка M(x, y, z) лежит на плоскости. Уравнение (3) есть уравнение первой степени относительно x, y, z, то есть всякая плоскость может быть представлена уравнением первой степени. |
|
|
|
|
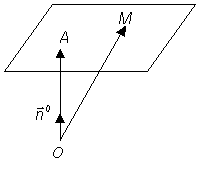 Рис.
1
Рис.
1