2.3.3. Исследование
общего уравнения
плоскости.
Пусть плоскость задана
общим уравнением
Ax + By + Cz + D = 0.
Выясним,
какие частные положения относительно
осей координат занимает плоскость,
если некоторые коэффициенты этого
уравнения обращаются в ноль.
- D = 0. Уравнение плоскости
принимает вид:
Ax + By + Cz
= 0.
Этому уравнению удовлетворяет
точка О(0, 0, 0), поэтому плоскость
проходит через начало координат.
- С = 0. Уравнение плоскости
примет вид:
Ax + By + D = 0.
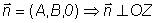 а сама плоскость
параллельна оси OZ.
а сама плоскость
параллельна оси OZ.
Аналогично
рассуждая, получим:
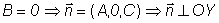 плоскость параллельна оси OY.
плоскость параллельна оси OY.
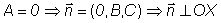 плоскость параллельна оси OX
плоскость параллельна оси OX
- D = C = 0. Уравнение плоскости
примет вид:
Ax + By = 0.
Это уравнение плоскости,
проходящей через начало координат и
параллельной оси OZ, то есть это будет плоскость,
проходящая через ось OZ.
Аналогично, если B = C = 0,
уравнение плоскости будет:
Ax + D = 0,
то есть плоскость проходит
через ось OY.
Наконец, если A = D = 0, Уравнение
плоскости будет:
By + Cz = 0.
то есть плоскость проходит
через ось OX.
- Если равны нулю два
коэффициента при текущих
координатах, то уравнение определяет
плоскость, параллельную
координатным плоскостям:
 -
плоскость параллельна
плоскости XOY. -
плоскость параллельна
плоскости XOY.
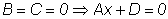 -
плоскость параллельна
плоскости ZOY. -
плоскость параллельна
плоскости ZOY.
 -
плоскость параллельна
плоскости XOZ. -
плоскость параллельна
плоскости XOZ.
- Если
 -
это уравнение плоскости YOZ. -
это уравнение плоскости YOZ.
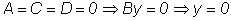 -
это уравнение плоскости XOZ. -
это уравнение плоскости XOZ.
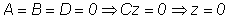 -
это уравнение плоскости XOY. -
это уравнение плоскости XOY.
|
 Плоскость
и виды ее уравнения в пространстве.
Плоскость
и виды ее уравнения в пространстве.