Лекция 2.3.

Плоскость и виды ее уравнения в пространстве.

2.3.4. Уравнение плоскости в отрезках.

Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Уравнение этой плоскости можно записать в общем виде:

Ax + By + Cz + D = 0,

(1)

где ни один из коэффициентов не равен нулю. Обозначим через a, b, c - величины отрезков, отсекаемых плоскостью на осях координат (рисунок 1).

Рис.1

Так как точка А(а. 0. 0) лежит на плоскости, то ее координаты удовлетворяют уравнению (1):

Aа + B0 + C0 + D = 0,

(2)

Аналогично, подставляя координаты точек B(0, b, 0) и C(0. 0, c) в уравнение плоскости, получим:

	(3)
	(4)

Подставляя равенства (2), (3), (4) в (1), получим:

так как

(5)

Это и есть уравнение плоскости в отрезках.

Пример: Уравнение плоскости 3x - 4y + z - 5 = 0, написать в отрезках.

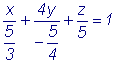- уравнение в отрезках, где  .