| Темы | Предыдущая лекция | Следующий пункт |Литература | ||||||||||||||
|
|
||||||||||||||
 Кривые
второго порядка.
Кривые
второго порядка.
|
||||||||||||||
|
2.2.1 Окружность. Эллипс. Окружностью называется геометрическое место точек на плоскости, равноудаленных от точки А(a, b) на расстояние R. Из
определения следует, что для любой
точки М(x, y), принадлежащей
геометрическому месту точек,
справедливо равенство: AM = R. Так
как
Это геометрическое место точек есть окружность радиуса R и с центром в точке A(a, b), равенство (1) есть уравнение окружности.
Пример 1.
Найти координаты центра и радиус
окружности: Решение: Разделив уравнение на 9 и сгруппировав члены уравнения, получим:
Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина. Эта постоянная больше расстояний между фокусами. Фокусы эллипса принято обозначать через
Пусть М – произвольная
точка эллипса с фокусами
Расстояние Так как Из определения эллипса
непосредственно вытекает следующий
способ построения его при помощи нити:
если концы нерастяжимой нити длины 2а
закрепить в точках Выведем уравнение эллипса. Возьмем на плоскости произвольную точку М и обозначим ее координаты через x и y. Обозначим через
В равенстве (3) заменим
переменные
Заменяя в равенстве (3)
или
Возведем в квадрат обе части последнего равенства, найдем:
Обозначим
Уравнению (6) можно придать вид:
или
Уравнение (7) называется каноническим уравнением эллипса. Это уравнение второй степени. Таким образом, эллипс есть линия второго порядка. В частном случае, когда b = a, уравнение эллипса примет вид:
Такое уравнение определяет окружность радиуса а. Эксцентриситет эллипса. Эксцентриситетом эллипса называется отношение расстояния между фокусами эллипса к длине его большой оси:
Так как c < a, то
Отсюда: Следовательно
эксцентриситет определяется
отношением осей эллипса, а отношение
осей, в свою очередь, определяется
эксцентриситетом. Таким образом,
эксцентриситет характеризует форму
эллипса, чем больше эксцентриситет, тем
больше эллипс вытянут. В случае
окружности b = a и Фокальные радиусы эллипса определяются по формулам:
Уравнение директрисы эллипса
Решение.
Для составления уравнения
эллипса надо знать его полуоси a и b. По условию 2а = 12, а = 6. Полуось
b находим из соотношения
Имеем
уравнение эллипса: Эксцентриситет
эллипса: |
|
|
|
|
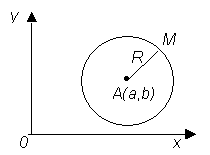
 Рис.
1.
Рис.
1.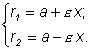 .
.