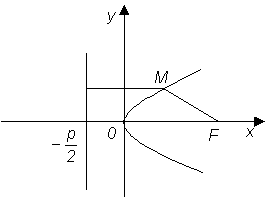
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости равно расстоянию до прямой .

Возьмем на плоскости произвольную точку М с координатами (x, y). По условию MF = d.

Так как , а то получим равенство:

,

или

(1)

Точка называется фокусом параболы, а прямая - ее директрисой. Отрезок MF = r - фокальный радиус параболы, причем .

Уравнение является уравнением параболы, симметричной относительно оси ординат.