ODE Lecture 6.1.

Темы | Предыдущий пункт | Следующий пункт | Литература

Лекция 2.2.

Кривые второго порядка.

2.2.2 Гипербола.

Гиперболой называется геометрическое место точек, для которых разность расстояний до двух точек постоянна и равна 2а ( a < c). Пусть M (x, y) - произвольная точка кривой, тогда по условию имеем:

а так как:

то предыдущее равенство примет вид:

или

После тождественных преобразований уравнение примет вид:

(1)

Обозначим . Так как с > а, то , а значит величина b вещественна и . Уравнение (1) примет вид:

или

(2)

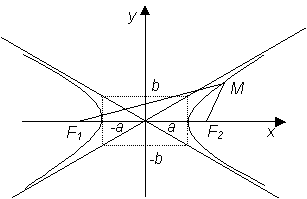
Уравнение (2) есть каноническое уравнение гиперболы, график которой представлен на рисунке:

Точки называются фокусами гиперболы. Числа a, b - длины соответственно действительной и мнимой полуосей. Число называется эксцентриситетом гиперболы. Так как .

Точки пересечения гиперболы с осью абсцисс (а, 0), (- а, 0) называют вершинами гиперболы, а точка О(0, 0) – ее центром. Гипербола имеет 2 асимптоты, уравнения которых имеют вид:

Отрезки есть фокальные радиусы точки М гиперболы.

Для правой ветви гиперболы:

Для левой ветви гиперболы:

Гипербола с фокусами на оси OY имеет уравнение:

Пример. Составить уравнение гиперболы, если ее фокусы лежат на оси OY и расстояние между ними равно 20. Действительная ось гиперболы равна 16.

Решение. Уравнение гиперболы в этом случае будет иметь вид:

где b – действительная, а – мнимая полуось гиперболы. Согласно условию 2с = 20; с = 10; b = 16; b = 8. Мнимую полуось найдем из соотношения:

Уравнение гиперболы будет:

Задачи для самостоятельного решения.