| Темы | Следующий пункт | Литература |
|
|
 Уравнение
прямой на плоскости.
Уравнение
прямой на плоскости.
|
|
2.1.1 Координаты на прямой и плоскости. Основная идея метода координат заключается в определении положения точки на прямой, на плоскости и в пространстве числами – ее координатами. Положение точки на прямой можно определить одним числом. Для этого возьмем на данной прямой некоторую точку О за начальную и выберем на этой прямой положительное направление и масштаб. Положение точки А относительно точки О определяется отрезком ОА (рис.1).
Число а расстояние между двумя точками по формуле:
М1М2 = Для определения положения точки на плоскости пользуются прямоугольной или декартовой системой координат, которая состоит из двух взаимно перпендикулярных направленных прямых, называемых осями координат. Прямая ОХ называется осью абсцисс, ОY – осью ординат. Точка их пересечения О называется началом координат. Единица масштаба l. Положение точки М относительно прямоугольных осей координат определяется двумя числами: координатами точек P и Q (рис. 2). Эти два числа X и Y называются координатами точки М и записываются так: М (Х; Y). Полярная система координат. Для определения положения точки на плоскости кроме прямоугольной системы координат часто употребляется полярная система координат. Элементами полярной системы координат являются точка О, называемая полюсом, луч ОР, называемый полярной осью и единица меры l (рис. 3).
Положение точки М на плоскости определяется
расстоянием этой точки до полюса, полярным радиусом
Если полярную ось взять за ось абсцисс прямоугольной системы координат, а полюс за начало координат, то связь между полярными и прямоугольными координатами точки устанавливается формулами:
|
|
|
|
|
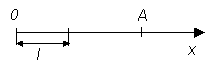 Рис.
1.
Рис.
1. Рис. 2.
Рис. 2.
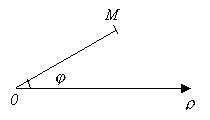 Рис.3.
Рис.3.
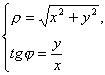
 Рис.4.
Рис.4.