| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||
|
|
||||

Уравнение прямой на плоскости. |
||||
|
2.1.4 Общее уравнение прямой. Прямая, как линия первого порядка. Теорема. В декартовых координатах каждая прямая определяется уравнением первой степени и обратно, каждое уравнение первой степени определяет некоторую прямую. Доказательство. Сначала докажем первое утверждение теоремы. Пусть дана произвольная прямая. Если эта прямая не перпендикулярна к оси OX, то она определяется уравнением y = kx + b, то есть уравнением первой степени. Если прямая перпендикулярна к оси OX то все ее точки имеют одинаковые абсциссы, равные величине отрезка, отсекаемого прямой на оси OX. (рис.1) ; таким образом, если мы обозначим величину этого отрезка буквой а, то получим уравнение прямой в виде x = a, что так же есть уравнение первой степени.
Итак, каждая прямая в декартовых координатах определяется уравнением первой степени; тем самым первое утверждение теоремы доказано. Докажем обратное утверждение. Пусть дано уравнение первой степени
с какими угодно численными значениями А, В, С. Если В не равно 0, то данное уравнение можно записать в виде:
Обозначая Если В = 0, то А не равно 0, и уравнению (1) можно придать вид: x = Обозначим Итак, каждое уравнение первой степени определяет прямую. Теорема доказана. Уравнение Ax + By + C = 0 называется общим уравнением прямой. При различных численных значениях А, В, С оно может определять всевозможные прямые. Неполное уравнение первой степени. Уравнение прямой в отрезках. Рассмотрим три частных случая, когда уравнение первой степени является неполным. 1) С = 0; уравнение имеет вид Ах + Ву = 0 и определяет прямую, проходящую через начало координат. 2) В = 0; x = 3) А = 0; .y = Пусть теперь дано уравнение Ax + By + C = 0 при условии, что ни один из коэффициентов не равен 0. Такое уравнение может быть приведено к некоторому специальному виду, который бывает удобен в ряде задач аналитической геометрии. Перенесем свободный член С в правую часть уравнения; получим: Ax + By = - С . Поделим затем обе части на – С, тогда будем иметь:
Вводя обозначения:
Здесь а и b есть величины отрезков, которые прямая отсекает на координатных осях, считая каждый от начала координат (рис. 2).
Чтобы убедиться в этом найдем точки пересечения прямой с координатными осями. Точка пересечения прямой с осью ОХ определяется путем совместного решения уравнения этой прямой и уравнения оси ОХ:
Отсюда: x = a, y = 0. Таким образом, величина отрезка, отсекаемого прямой на оси ОХ, действительно равна а. Аналогично устанавливается, что величина отрезка, отсекаемого прямой на оси ОY, равна b. Уравнение вида (2) принято называть уравнением прямой «в отрезках». Эту форму уравнения удобно использовать для построения прямой на чертеже.
Пример. Дана прямая 3x - 5y + 15 = 0. Составить для этой прямой уравнение «в отрезках» и построить. Решение. Число 15 перенесем в правую часть:3x - 5y = - 15, и поделим каждое слагаемое на –15:
Если отложим на координатных осях OX и OY отрезки, величины которых соответственно равны a = - 5 и b = 3 и соединим их концы, то получим искомую прямую (рис. 3).
|
|
|
|
|
 Рис.
1.
Рис.
1.
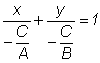 .
.
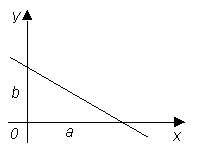 Рис.
2.
Рис.
2.
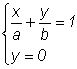
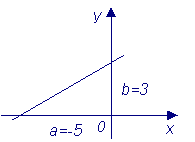 Рис.
3.
Рис.
3.