| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||
|
|
||||
 Уравнение
прямой на плоскости.
Уравнение
прямой на плоскости.
|
||||
|
2.1.3 Вычисление угла между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Одной из стандартных задач аналитической геометрии является вычисление угла между двумя прямыми. Выведем формулу, по которой можно вычислить угол между прямыми, зная их угловые коэффициенты ( предполагаем, что ни одна из прямых не перпендикулярна оси OX). Рассмотрим две прямые; будем одну из них (какую
угодно) называть первой, другую второй.
Обозначим соответственно, через k1 и
k2
угловые коэффициенты этих
прямых, через
Но
Это и есть формула, которую мы хотели получить. В случае
Пример 1.
Определить угол между прямыми: Решение.
По формуле (1) находим: Таким образом, один из углов, которые составляют
данные прямые, равен При решении различных задач аналитической геометрии часто бывает важно, зная уравнения двух прямых, установить, являются ли они параллельными или перпендикулярными друг другу. Пусть известны угловые
коэффициенты двух прямых k1 и
k2
. Обозначим через
Данные прямые
перпендикулярны тогда, когда угол
Следовательно, признаком перпендикулярности двух прямых является соотношение:
Таким образом, условие перпендикулярности двух прямых формулируют так: угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
Применяя это правило сразу
можно сказать, что, например, прямые
Пример 2. Найти проекцию точки Р(4, 9) на прямую, проходящую через точка А(3, 1) и В(5, 2). Решение. Искомую точку найдем, решая совместно уравнение прямой АВ и уравнение перпендикуляра, проведенного к этой прямой из точки Р. Прежде всего составим уравнение прямой АВ:
Теперь составим уравнение перпендикуляра из точки Р на прямую АВ, напишем уравнение произвольной прямой, проходящей через точку Р, используя формулу (4) параграфа 2.1.2:
где k пока еще
неопределенный угловой коэффициент.
Искомая прямая перпендикулярна к
прямой АВ, следовательно ее угловой
коэффициент должен удовлетворять
условию перпендикулярности с прямой АВ.
Так как угловой коэффициент прямой АВ
равен
Решая совместно уравнения |
|
|
|
|
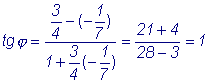 .
. 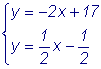 получим
координаты проекции: x = 7, y = 3.
получим
координаты проекции: x = 7, y = 3.