| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||||
|
|
||||||
 Распределение
случайных величин
Распределение
случайных величин
|
||||||
|
13.5.3 Равномерное распределение На практике это распределение встречается тогда, когда среди принимаемых случайными величинами значений нет каких либо предпочтительных. В частности, обычно считают, что события, происходящие в произвольные моменты времени с равной вероятностью могут происходить в любой момент времени.
Определение.
Непрерывная случайная величина Х имеет
равномерное распределение на
интервале
где С - const. График плотности f(x) равномерного распределения изображен на рисунке 1.
Найдем значение постоянной С из условия, что площадь, ограниченная кривой распределения, равна единице.
Отсюда
Найдем выражение функции распределения F(х) для равномерного закона распределения
Таким образом, имеем
График функции F(x) изображен на рисунке 2. Определим основные числовые характеристики случайной величины Х, имеющей равномерное распределение. Математическое ожидание
Итак, математическое ожидание
равномерного распределения находится
посередине интервала Моды равномерное распределение не имеет. Дисперсию случайной величины Х находим по формуле
То есть Вероятность попадания случайной
величины Х, имеющей равномерное
распределение, на отрезок
Примером реальных ситуаций, связанных с необходимостью рассмотрения равномерно распределенных случайных величин, могут служить: ошибка при снятии показаний с измерительных приборов, если производится округление отсчета до ближайшего целого деления; время ожидания <обслуживания> при точно периодическом (через каждые Т единиц времени) включении (прибытии) <обслуживающего устройства> и при случайном поступлении (прибытии) заявки на обслуживание в этом интервале; описание погрешностей аналого - цифрового преобразования; рассмотрение гармонических колебаний со случайной фазой. Равномерное распределение иногда используется в качестве "нулевого приближения" в описании априорного распределения анализируемых параметров в так называемом байесовом подходе в условиях полного отсутствия априорной информации об этом распределении.
|
|
|
|
|
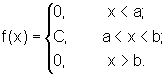
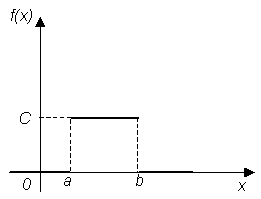
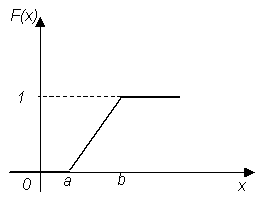
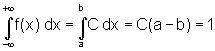 ,
,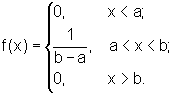
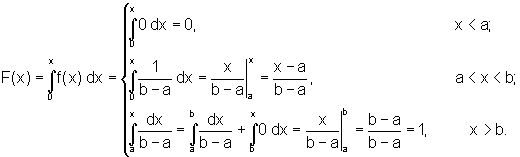
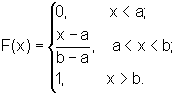
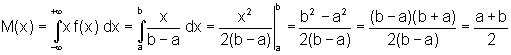 .
.