Рассмотрим теперь линейное однородное уравнение второго порядка
с постоянными коэффициентами, т.е. уравнение
 ,
где p и q - постоянные числа.
,
где p и q - постоянные числа.
Чтобы найти общее решение этого уравнения, достаточно найти два линейно
независимых частных решения.
Заметим, что функция, удовлетворяющая линейному однородному уравнению,
должна быть подобна своим производным. Таким свойством обладает, как
известно, показательная функция. Это соображение наталкивает на мысль
искать частные решения в виде y = e kx ,
где k=const .
Подставляя эту функцию и ее производные
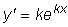 и
и
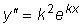
в рассматриваемое уравнение,
получим:
 .
.
Так как
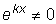 ,
,
значит
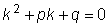 .
.
Следовательно, если k будет удовлетворять полученному уравнению,
которое называется характеристическим , то
y = e kx будет решением исходного уравнения.
Характеристическое уравнение есть квадратное уравнение, имеющее два
корня: обозначим их через
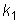 и
и
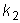 . При этом
. При этом
 .
.
Здесь возможны следующие случаи:
1. 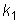 и
и
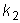 - действительные и притом не равные между собой числа
- действительные и притом не равные между собой числа
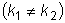 .
.
2. 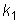 и
и
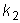 - действительные равные числа
- действительные равные числа
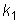 =
=
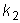 .
.
3. 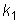 и
и
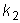 - комплексные числа.
- комплексные числа.
Рассмотрим каждый случай отдельно.
1. Корни характеристического уравнения действительны и различны.
В этом случае частными решениями будут функции
 и
и
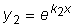 .
.
Причем эти решения
линейно независимы, т.к.
 .
.

Пример
Дано уравнение  .
.
Характеристическое уравнение имеет вид
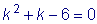 .
.
Корни характеристического уравнения:
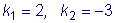 . Общее решение:
. Общее решение:
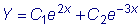 .
.
2. Корни характеристического уравнения действительные и равные.
В этом случае мы имеем только одно частное решение
y = e kx , т.к.
k1 = k2 = k .
Для построения общего решения нужно найти еще одно частное решение,
линейно независимое с первым. Будем искать второе решение в виде
 ,
,
где U(x) - неизвестная функция, подлежащая определению.
Подставляя функцию

и ее производные
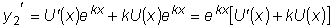 ,
,
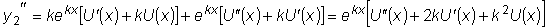
в рассматриваемое линейное однородное уравнение, получим:
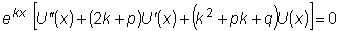 .
.
Так как k - кратный корень характеристического уравнения,
то 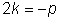 или
или
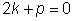 и
и
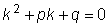 .
.
Следовательно, для определения функции U(x) получаем уравнение
 или
или
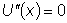 . Интегрируя, получаем:
. Интегрируя, получаем:
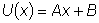 .
.
В частности, можно положить
A =1, B =0 ; тогда
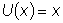 .
.
Таким образом, в
качестве второго частного решения можно взять
 .
.
Это решение линейно
независимо с первым, т.к.
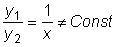 .
.
Поэтому общее решение будет
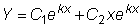 .
.

Пример
Дано уравнение
 .
.
Характеристическое уравнение имеет вид
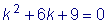 .
.
Корни характеристического
уравнения:
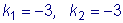 . Общее решение:
. Общее решение:
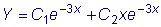 .
.
3. Корни характеристического уравнения комплексные.
Так как коэффициенты p и q характеристического
уравнения действительные числа, то комплексные корни будут сопряженными.
Причем,
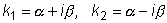 , где
, где
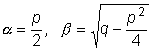 .
.
Частные решения можно записать в форме
 .
.
Построение общего
решения по этим частным решениям представляется не очень удобным, т.к.
эти решения являются функциями, принимающими комплексные значения.
Однако мы можем с их помощью получить два действительных частных решения.
Для этого нам понадобятся формулы Эйлера :
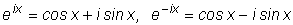 .
.
В справедливости этих формул можно убедиться следующим образом.
Рассмотрим функцию

и найдем ее производную:
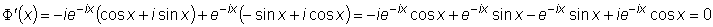 .
.
Отсюда следует, что  .
.
Но  , следовательно,
, следовательно,
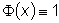 , т.е.
, т.е.
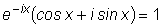
или
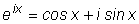 .
.
Получили первую из формул Эйлера.
Подставляя теперь в эту формулу -x вместо x,
получим вторую формулу
 .
.
Используя формулы Эйлера,
перепишем теперь частные решения
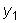 и
и
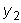 в виде
в виде
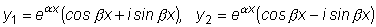 .
.
Полусумма этих решений
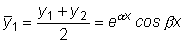
также будет решением
рассматриваемого уравнения, что вытекает из свойств решений линейного
однородного уравнения. Точно так же решением будет функция
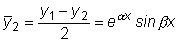 .
.
Эти решения являются функциями, принимающими действительные значения (при действительных
значениях x ).
Кроме того, эти два решения линейно независимы, т.к.
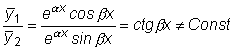 .
.
Следовательно, общее решение в рассматриваемом случае имеет вид
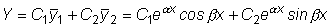
или, окончательно,
 .
.

Пример
Найти частное решение уравнения
 ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
 .
.
Составим характеристическое уравнение
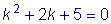 .
.
Найдем его корни
 .
.
Следовательно, общее решение есть
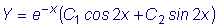 .
.
Найдем теперь
частное решение, удовлетворяющее заданным начальным условиям.
На основании первого условия находим
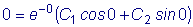 ,
,
откуда
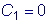 .
.
Заметив, что
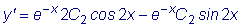 ,
,
из второго условия получаем:
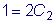 , т.е.
, т.е.
 .
.
Таким образом, искомое частное решение есть
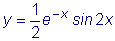 .
.

 ,
где p и q - постоянные числа.
,
где p и q - постоянные числа.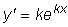 и
и
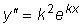
 .
. 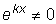 ,
, 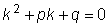 .
. 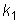 и
и
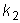 . При этом
. При этом  .
. 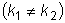 .
.  и
и
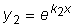 .
.  .
.
 .
. 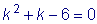 .
. 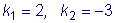 . Общее решение:
. Общее решение: 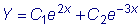 .
.  ,
, 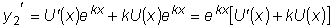 ,
,
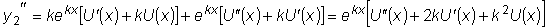
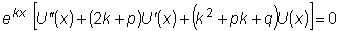 .
. 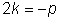 или
или
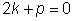 и
и  или
или
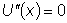 . Интегрируя, получаем:
. Интегрируя, получаем:
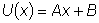 .
. 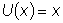 .
.  .
. 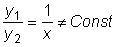 .
. 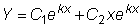 .
. .
.
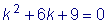 .
. 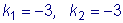 . Общее решение:
. Общее решение: 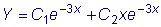 .
. 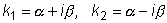 , где
, где 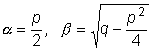 .
.
 .
. 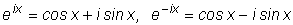 .
. 
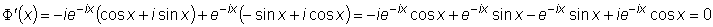 .
.
 .
.
 , следовательно,
, следовательно,
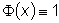 , т.е.
, т.е.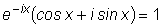
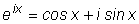 .
.
 .
.
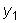 и
и
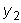 в виде
в виде
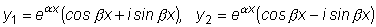 .
. 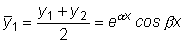
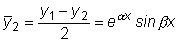 .
.
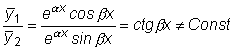 .
.
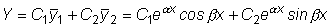
 .
. ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
 .
. 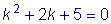 .
.
 .
.
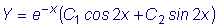 .
. 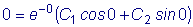 ,
,
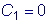 .
.
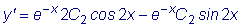 ,
, 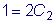 , т.е.
, т.е.  .
.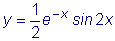 .
.