| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения высших порядков |
|
|
|
|
6.2.5. Линейные неоднородные уравнения второго порядка |
|
Рассмотрим линейное неоднородное уравнение второго порядка
Теорема.
Общее решение линейного неоднородного уравнение представляется как сумма
какого-нибудь частного решения этого уравнения и общего решения
соответствующего однородного уравнения, т.е.
y = Y + y* ,
Доказательство.
Докажем сначала, что функция y*
является решением рассматриваемого уравнения. Подставляя
y = Y + y* в исходное уравнение, получим:
Из этой системы уравнений нужно определить
Переписав систему в виде
замечаем, что определитель
этой системы есть определитель Вронского для функций
При этих значениях
Таким образом, доказано, что решение неоднородного уравнения есть сумма y = Y + y* .
|
|
|
|
|
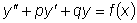 .
Структура общего решения такого уравнения определяется следующей
теоремой.
.
Структура общего решения такого уравнения определяется следующей
теоремой.
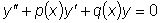 и
и
 .
.  . Общее решение линейного
однородного уравнения можно представить в форме
. Общее решение линейного
однородного уравнения можно представить в форме
 , где
, где
 и
и
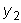 линейно независимые
решения этого уравнения, а
линейно независимые
решения этого уравнения, а
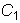 и
и
 произвольные постоянные.
произвольные постоянные.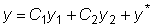 .
. 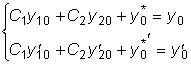 .
.

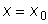 .
Так как эти функции линейно независимы, то определитель Вронского не
равен нулю. Следовательно, система имеет определенное решение
.
Так как эти функции линейно независимы, то определитель Вронского не
равен нулю. Следовательно, система имеет определенное решение
 ,
,
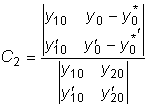 .
.