Рассмотрим линейное уравнение n -го порядка
 ,
,
где
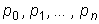 - постоянные.
- постоянные.
Уравнение такого вида называется уравнением
Коши
-
Эйлера.
Это уравнение с переменными коэффициентами, но оно легко приводится к
уравнению с постоянными коэффициентами с помощью подстановки
x = et (x > 0).
В самом деле из этого равенства находим:
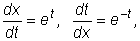


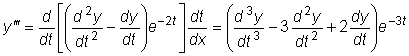 .
.
При подстановке всех этих величин в исходное уравнение там произойдет
сокращение показательных множителей и мы получим уравнение с постоянными
коэффициентами.
Мы рассмотрели подстановку x = et
считая, что x > 0, а если x < 0, то используется
подстановка x = - et.

Пример
Решить уравнение
 .
.
Для x > 0 полагаем x = e t .
Тогда
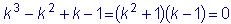
или

 .
.
Подставляя все эти выражения в исходное уравнение, получим:
 .
.
Это линейное уравнение с постоянными коэффициентами.
Находим общее решение линейного однородного уравнения:
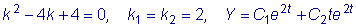 .
.
Частное решение
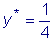
находится легко.
Следовательно,
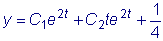 .
.
Возвращаясь к переменной x , получаем:
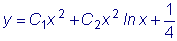 .
.
Это общее решение
заданного уравнения для x>0.
Рассмотрим теперь случай x<0.
Полагая x = - e t, t = ln ( -x ), находим:
 .
.
Подставляя все эти выражения в исходное уравнение, получим:
 .
.
Получили такое же уравнение,
как и в первом случае. Следовательно, общее решение его нам уже известно
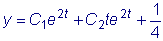 .
.
Возвращаясь к переменной x , получим:
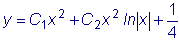 - общее решение заданного уравнения для x < 0.
- общее решение заданного уравнения для x < 0.

 ,
, 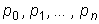 - постоянные.
- постоянные. 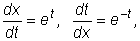


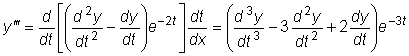 .
.  .
.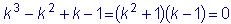

 .
.  .
.
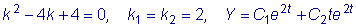 .
. 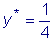
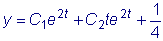 .
.
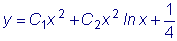 .
.  .
.
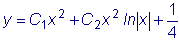 - общее решение заданного уравнения для x < 0.
- общее решение заданного уравнения для x < 0.