| Темы | Предыдущий пункт | Следующая лекция | Литература |
|
|

Элементы линейной алгебры |
|
1.1.6 Метод Гаусса. Теорема Кронекера - Капелли Обратимся снова к
задаче решения системы линейных алгебраических уравнений размерностью
видим, что если закрепить раз и навсегда нумерацию неизвестных, то можно вообще опустить неизвестные в записи системы и записать ее в виде матрицы, отделяя столбец свободных членов вертикальной чертой. Система запишется в виде матрицы
которую будем называть расширенной матрицей системы. Ясно, что система восстанавливается по своей расширенной матрице однозначно. Именно в такой форме вводится информация при решении линейных алгебраических уравнений на ЭВМ методом Гаусса. Рассмотрим примеры решения и исследования системы линейных алгебраических уравнений методом последовательного исключения неизвестных Гаусса. Пусть необходимо решить систему:
Рассматриваемой системе соответствует матрица: 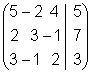 . .
Над этой матрицей мы будем производить эквивалентные преобразования, конечной целью которых будет получение верхнетреугольной матрицы, у которой все элементы, стоящие под главной диагональю обратятся в нуль. Преобразования стараются производить так, чтобы на главной диагонали появлялись единицы. Как получить в левом верхнем углу единицу ? Конечно, самый легкий способ - поделить первую строку на 5. Однако удобнее избегать таких преобразований, которые нарушают целочисленность элементов матрицы. В данном случае к цели приводит вычитание из первой строки второй, умноженной на 2, после этого матрица принимает вид:
Теперь, в соответствии со схемой, из второй строки вычитается первая, умноженная на 2, а из третьей первая, умноженная на 3, после чего матрица принимает вид:
Для того, чтобы на том месте, где стоит 19, получить единицу, можно проделать такие преобразования: во-первых, из третьей строки вычесть вторую
и, во-вторых, из второй строки вычесть третью, умноженную на 5, после чего дальнейшие преобразования очевидны:
Последней матрице соответствует система уравнений
из которой легко находим:
Итак,
рассматриваемая система имеет единственное решение:
В приведенном
примере число уравнений было равно числу неизвестных, однако, при
решении систем с размерами
Пусть система имеет вид:
Выписываем ее в
виде расширенной матрицы и проводим все преобразования методом
исключения над этой матрицей ( ведущие элементы выделены скобками
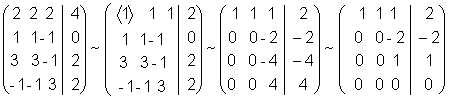 . .
Прямой ход метода
исключения выполнен полностью. Получили систему так называемого
треугольного вида. Что можно отметить на данном этапе ? Последнее
уравнение обратилось в тождество. Коэффициент у
Из полученной
системы видно, что она имеет множество решений (не определена). Одна
из переменных
Перенесем свободную неизвестную в правую часть системы (ибо она же является неизвестной величиной) и переставим уравнения (строки) так, чтобы базисные неизвестные оказались в первых строках:
Сделав это, мы
фактически привели систему к квадратичному виду - из двух уравнений с
двумя неизвестными
Ранг матрицы
A показывает сколько переменных нужно взять в
качестве базисных. Остальные
n - r переменных будут свободными. Отметим, что согласно
своему определению
Рангом матрицы называется наивысший порядок отличных от нуля определителей, полученных по правилу: их элементы стоят на пересечении выделенных строк и столбцов матрицы. Эти определители называются минорами матрицы. Минор имеет порядок k, если он стоит на пересечении k строк и k столбцов матрицы. Определитель, порядок которого равен рангу матрицы, называется базисным минором матрицы. Он может быть не единственным. Можно показать, что элементарные преобразования не меняют ранга матрицы. Поэтому, когда требуется вычислить ранг матрицы, его определяют, преобразуя матрицу по методу исключения Гаусса. Вернемся к системе линейных
уравнений. Обратим внимание, что rA =
rB. Это не случайно. Отличными от миноров матрицы
A минорами матрицы
B будут только те определители, которые содержат
часть столбца свободных членов. Поэтому, чтобы найти в матрице
B определитель порядка k > rA нужно взять базисный минор
A и добавить к нему строку и часть столбца свободных
членов. Коэффициенты левой части в строке равны нулю (почему ?).
Поэтому мы должны взять такую строку, в которой свободный член не
равен нулю (иначе она будет нулевой и минор будет равняться нулю).
Таким образом, строка должна иметь вид
Все сказанное есть наводящие соображения к теореме, носящей название:
Теорема Кронекера - Капелли. Для того, чтобы система линейных алгебраических уравнений имела решение (была совместна), необходимо и достаточно, чтобы ранг расширенной матрицы системы равнялся рангу матрицы коэффициентов: rA = rB. Отметим также, что если rA = rB = n, то система совместна и не имеет свободных переменных, т.е. имеет единственное решение (определена). При решении систем линейных алгебраических уравнений нет необходимости заранее вычислять ранги rA и rB. Их определение производится автоматически при выполнении метода исключения Гаусса. В нашем случае rA = rB = r = 2 < n. Система совместна и неопределенна. Она приводится к виду:
где c - произвольное число. Запишем решения
системы, обозначая свободную переменную
В данной формуле
содержатся все решения данной системы уравнений, вследствие чего она
называется общим решением неоднородной системы и обозначается
Проанализируем
составляющие
Вектор-столбец
 . .
Вектор
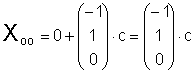
давало бы все
решения однородной системы. Поэтому данное слагаемое называется общим
решением однородной системы. Итак
Как мы убедились, метод исключения Гаусса позволяет полностью исследовать и решить систему линейных алгебраических уравнений. Отметим, что если вести эквивалентные преобразования до получения на месте матрицы A единичной матрицы E, то на месте матрицы B появится решение - матрица X. Такой метод решения называется методом Гаусса - Жордана. |
|
|
|
|

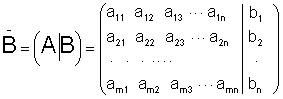 ,
,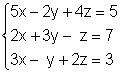 .
.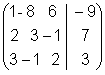 .
. .
.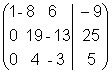
 .
. ,
,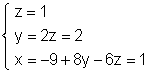 .
.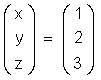 .
. .
. .
. .
.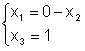 или
или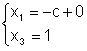 ,
,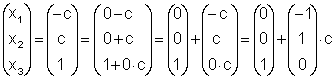 .
. .
.