| Темы | Предыдущий пункт | Следующий пункт | Литература | |||
|
|
|||

Элементы линейной алгебры |
|||
|
1.1.5 Метод обратной матрицы решения систем линейных уравнений. Систему линейных
уравнений AX = B можно решать различными способами. Если матрица
коэффициентов квадратная, т.е. число неизвестных в системе равно числу
уравнений ( Под обратной к данной квадратной матрице A матрицей А-1 подразумевают матрицу, которая будучи умножена как слева так и справа на данную матрицу A дает единичную матрицу:
где E - единичная матрица (нейтральный элемент относительно умножения матриц).  . .
Составим матрицу А-1
, обратную к
A и умножим слева обе части уравнения на
А-1, получим или, на основании правил,
или но E X = X, следовательно, Получив матрицу X по этому правилу, мы можем записать ее элементы
Итак, решение матричного уравнения можно получить после предварительного получения обратной матрицы. Обратная матрица имеет специальную структуру:
Для получения А-1 можно рекомендовать следующий алгоритм:
где
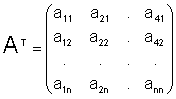
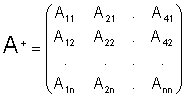 . .
Пример. Решить систему
уравнений:
Решение: Обозначим матрицу из коэффициентов при неизвестных через
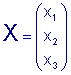 . .
Систему перепишем
в матричном виде: Следуя вышеприведенному алгоритму определим сначала  , а затем обратную матрицу: , а затем обратную матрицу:
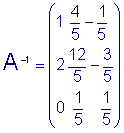 . .
Искомая матрица  . .
Ответ:
Метод обратной матрицы ограничен использованием только для систем размерностью
|
|
|
|
|
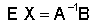 ,
, 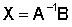 теряет смысл.
теряет смысл.
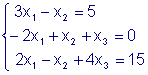 .
. матрицу из свободных членов:
матрицу из свободных членов:
 ,
, 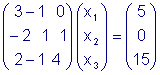 .
.