| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||
|
|
||||

Элементы линейной алгебры |
||||
|
1.1.2. Система из n уравнений с n неизвестными. Рассмотрим общую квадратную систему линейных алгебраических уравнений, т.е. систему, в которой число уравнений равно числу неизвестных:
Если
Для сокращения выкладок выпишем систему из трех уравнений с тремя неизвестными.
Применяя метод исключения Гаусса, систему (1.4) можно привести к треугольному виду: 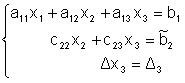
и, если Число

и вычисляется по правилам вычисления определителей 3-го порядка. Числа
Все четыре данных определителя имеют три строки и три столбца и называются определителем 3 - го порядка. Для системы третьего порядка будем иметь: 1) если 2) если 3) если В общем случае будем
иметь n + 1 определителей n - го порядка:
Формулы:
называются формулами Крамера. Таким образом, для квадратной системы линейных алгебраических уравнений имеются два, в каком -то смысле конкурирующих, метода. Первым является метод исключения Гаусса. Второй дает идея определителя. Чтобы воспользоваться вторым способом решения, надо иметь формулу для вычисления определителя произвольного n - го порядка и знать свойства определителей, которые могли бы быть использованы для облегчения процедуры их нахождения.
|
|
|
|
|

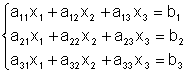
 ,
,
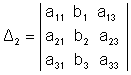 ,
,
