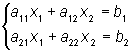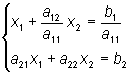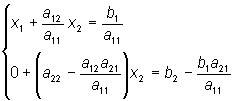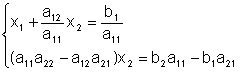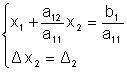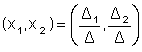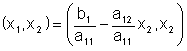| Темы | Следующий пункт | Литература | ||||
|
|
||||

Элементы линейной алгебры |
||||
|
1.1.1 Системы из двух линейных уравнений с двумя неизвестными. Центральная задача линейной алгебры - это решение систем линейных уравнений. Наиболее важным, и в то же время наиболее простым, является случай, когда число неизвестных n равно числу уравнений n. Возьмем сначала простейший случай, когда n = 2:
Числа аij называются коэффициентами при неизвестных. Первый индекс i указывает номер уравнения, в котором стоит коэффициент, второй j - номер неизвестного, на который аij домножается. Числа b1 и b2 в правой части называются свободными членами. Решение данной системы - это пара чисел х1 и х2, которая при подстановке обращает оба этих уравнения в тождества. При этом возможны случаи: - система несовместна, если она не имеет решения; - совместна, если она имеет решение; - неопределенна, если она совместна, но имеет множество решений; - определенна, если система совместна и имеет только одно решение. Для получения решения системы (1.1) исключим неизвестное х2 из уравнения
Здесь введены обозначения:
Если
Таким
образом, если
Если
Формулы
Легко
видеть, что он составляется из коэффициентов при неизвестных. Числа
Получаются они из главного определителя системы заменой столбца коэффициентов при соответствующей неизвестной столбцом свободных членов. Формулы Крамера позволяют найти единственное решение или установить ее несовместность, но не позволяют найти все множество решений в том случае, когда система неопределенна. Метод исключения неизвестных, метод Гаусса, которым мы пользовались для упрощения системы, является основным и универсальным вычислительным приемом линейной алгебры. Этот метод основан на теореме, которую приведем без доказательства.
Теорема. Следующие три операции приводят к системам, которые эквивалентны исходным (имеют те же решения): 1) отбрасывание в системе уравнения, все коэффициенты которого и свободный член равны нулю; 2) умножение какого-либо уравнения системы на число, отличное от нуля; 3) прибавление (почленное) к какому-либо уравнению системы другого уравнения системы. Так
как исключая неизвестные, мы пользовались только этими операциями, то из
теоремы следует, что вторая система всегда эквивалентна первой, а третья
эквивалентна второй и первой при
|
|
|
|
|