Методы интегрирования рациональных дробей рассмотрим на примерах.

Пример 1:
Найти 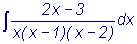
В предыдущем разделе 4.3.2 мы нашли разложение рациональной дроби,
стоящей в подынтегральном выражении на простые дроби
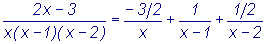
Теперь можно использовать это разложение для нахождения интеграла.
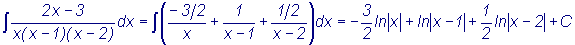

Пример 2:
Найти 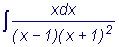
На основании теоремы о разложении правильной дроби в сумму простейших
дробей имеем

Приведя дроби в обеих частях последнего равенства к общему знаменателю,
имеем 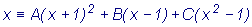 . При x =1 и x = - 1 находим,
что 4A = 1, -1 = -2B, то есть A = 1/4 и B = 1/2. Для нахождения С приравняем
коэффициенты при x2. Получим 0 = A + C, то есть C = -1/4.
Окончательно получим . При x =1 и x = - 1 находим,
что 4A = 1, -1 = -2B, то есть A = 1/4 и B = 1/2. Для нахождения С приравняем
коэффициенты при x2. Получим 0 = A + C, то есть C = -1/4.
Окончательно получим


Пример 3:
Найти 
 следовательно следовательно
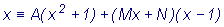 . При x = 1 получим 1 = 2A,
то есть A = 1/2. Далее . При x = 1 получим 1 = 2A,
то есть A = 1/2. Далее
 Откуда M = -1/2, N = 1/2. Откуда M = -1/2, N = 1/2.

 Задачи
для самостоятельного решения. Задачи
для самостоятельного решения.
|

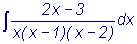
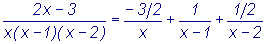
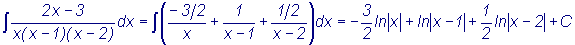
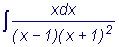

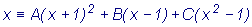 . При x =1 и x = - 1 находим,
что 4A = 1, -1 = -2B, то есть A = 1/4 и B = 1/2. Для нахождения С приравняем
коэффициенты при x2. Получим 0 = A + C, то есть C = -1/4.
Окончательно получим
. При x =1 и x = - 1 находим,
что 4A = 1, -1 = -2B, то есть A = 1/4 и B = 1/2. Для нахождения С приравняем
коэффициенты при x2. Получим 0 = A + C, то есть C = -1/4.
Окончательно получим 

 следовательно
следовательно 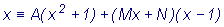 . При x = 1 получим 1 = 2A,
то есть A = 1/2. Далее
. При x = 1 получим 1 = 2A,
то есть A = 1/2. Далее Откуда M = -1/2, N = 1/2.
Откуда M = -1/2, N = 1/2. 