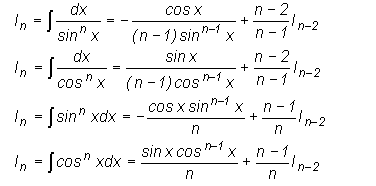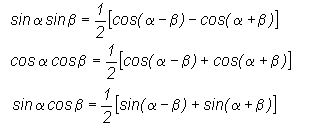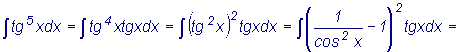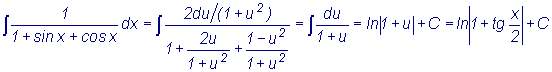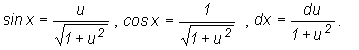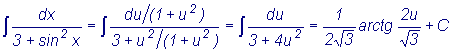1. При нахождении интегралов вида 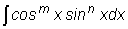 ,
,
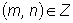 возможны следующие случаи:
возможны следующие случаи:
1) Одно из чисел m или n - нечетное. Тогда производится
"отщепление" одной из нечетных степеней с последующим внесением под знак
дифференциала.
2) Оба числа m и n - четные. Тогда рекомендуется использовать
тригонометрические формулы понижения степени.
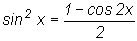 ,
, 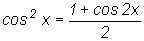 .
.

Пример
:

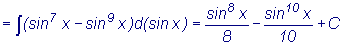
"Отщепление" степени лучше производить там, где показатель меньше.

Пример
:
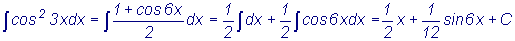
В ряде случаев полезны следующие рекуррентные соотношения, позволяющие
понизить показатель степени.
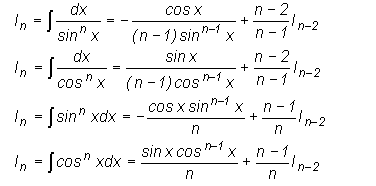
2. Интегралы вида 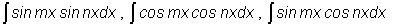 вычисляются на основании формул тригонометрии:
вычисляются на основании формул тригонометрии:
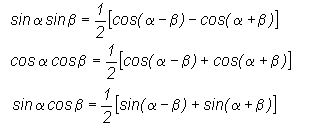

Пример
:
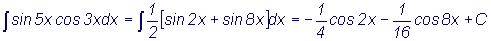
3. Интегралы вида 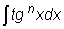 и
и
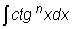 вычисляются путем "отщепления"
четной степени и использования тригонометрических формул
вычисляются путем "отщепления"
четной степени и использования тригонометрических формул 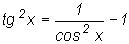 и
и 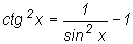 . После упрощения подынтегрального
выражения пользуются методом внесения функции под знак дифференциала
или вышеприведенными рекуррентными соотношениями.
. После упрощения подынтегрального
выражения пользуются методом внесения функции под знак дифференциала
или вышеприведенными рекуррентными соотношениями.

Пример
:
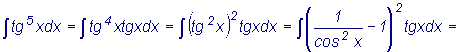
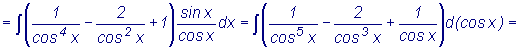
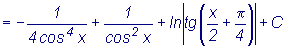
4. Интегралы вида 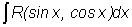 , где R
- рациональная функция, приводятся к интегралам от рациональных функций
новой переменной u с помощью универсальной тригонометрической подстановки
, где R
- рациональная функция, приводятся к интегралам от рациональных функций
новой переменной u с помощью универсальной тригонометрической подстановки
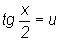 . В этом случае
. В этом случае
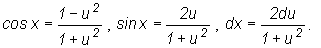

Пример
:
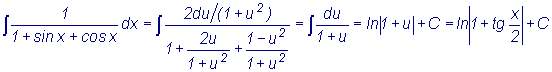
В случае, когда имеет место тождество 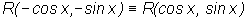 ,
для приведения подынтегральной функции к рациональному виду можно применять
упрощенную подстановку
,
для приведения подынтегральной функции к рациональному виду можно применять
упрощенную подстановку 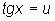 . При этом
. При этом
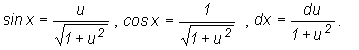

Пример
:
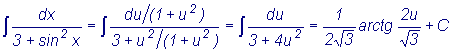
 Задачи
для самостоятельного решения.
Задачи
для самостоятельного решения.